Laminar flow describes the smooth, orderly movement of fluid particles in parallel layers with minimal mixing, commonly seen in low-velocity or highly viscous fluids. This flow pattern contrasts with turbulent flow and is crucial in applications like aircraft wing design, blood circulation analysis, and industrial fluid systems to reduce drag and maintain efficiency. Explore the rest of the article to understand how laminar flow impacts various engineering and scientific fields relevant to your interests.
Table of Comparison
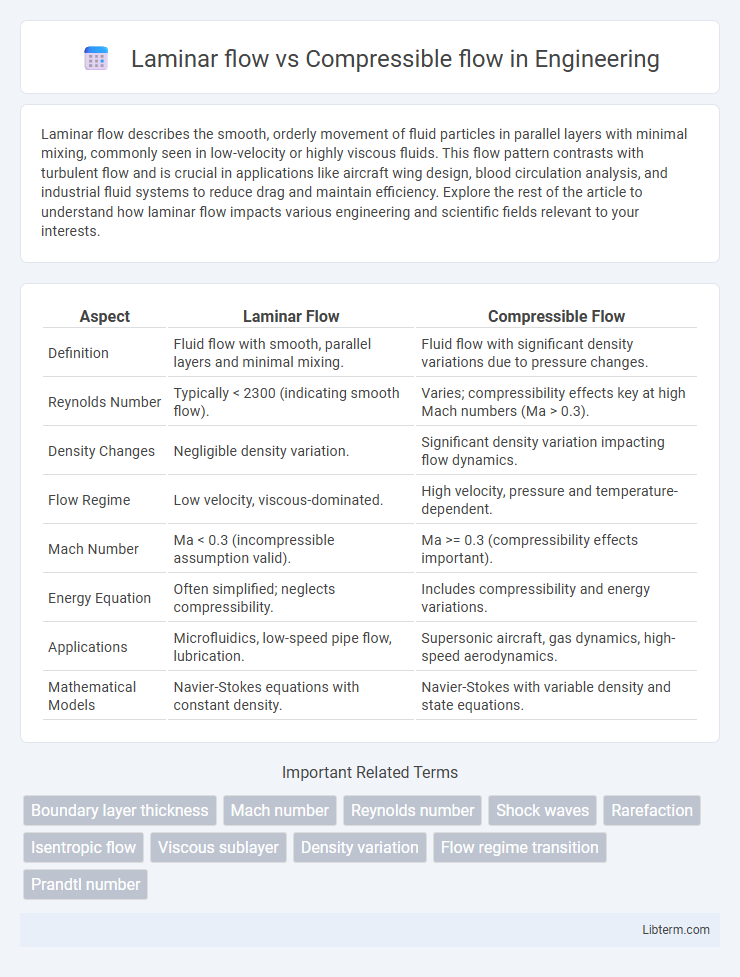
| Aspect | Laminar Flow | Compressible Flow |
|---|---|---|
| Definition | Fluid flow with smooth, parallel layers and minimal mixing. | Fluid flow with significant density variations due to pressure changes. |
| Reynolds Number | Typically < 2300 (indicating smooth flow). | Varies; compressibility effects key at high Mach numbers (Ma > 0.3). |
| Density Changes | Negligible density variation. | Significant density variation impacting flow dynamics. |
| Flow Regime | Low velocity, viscous-dominated. | High velocity, pressure and temperature-dependent. |
| Mach Number | Ma < 0.3 (incompressible assumption valid). | Ma >= 0.3 (compressibility effects important). |
| Energy Equation | Often simplified; neglects compressibility. | Includes compressibility and energy variations. |
| Applications | Microfluidics, low-speed pipe flow, lubrication. | Supersonic aircraft, gas dynamics, high-speed aerodynamics. |
| Mathematical Models | Navier-Stokes equations with constant density. | Navier-Stokes with variable density and state equations. |
Introduction to Fluid Flow Concepts
Laminar flow is characterized by smooth, orderly fluid motion with parallel layers and minimal mixing, typically occurring at low Reynolds numbers below 2,000. Compressible flow involves significant changes in fluid density, pressure, and temperature, commonly observed in gases at high velocities or under varying pressure conditions. Understanding these fundamental flow regimes is essential for analyzing fluid behavior in applications ranging from aerodynamic design to pipeline transport.
Defining Laminar Flow
Laminar flow is defined as a smooth, orderly fluid motion where layers of fluid move parallel without disruption between them, typically occurring at low Reynolds numbers below 2,000. This flow regime contrasts sharply with compressible flow, where fluid density changes significantly due to pressure variations, affecting velocity and requiring complex equations of state. Understanding laminar flow's stability and predictability is critical in applications such as microfluidics and heat exchanger design.
Understanding Compressible Flow
Compressible flow involves significant variations in fluid density, occurring at high velocities near or above the speed of sound, contrasting with laminar flow where density changes are negligible. Understanding compressible flow requires analyzing shock waves, expansion fans, and Mach number effects to predict pressure, temperature, and velocity changes accurately. Applications such as supersonic aircraft, gas pipelines, and nozzles depend on precisely modeling these compressible flow characteristics to optimize performance and ensure structural integrity.
Key Differences Between Laminar and Compressible Flow
Laminar flow is characterized by smooth, orderly fluid motion with parallel layers and low Reynolds numbers, whereas compressible flow involves significant density changes due to high velocities approaching or exceeding the speed of sound. Laminar flow primarily applies to incompressible fluids at low speeds, while compressible flow deals with gases experiencing shock waves, expansion fans, and variable thermodynamic properties. Key differences include velocity profiles, pressure variations, and fluid density behavior under varying flow conditions.
Governing Equations for Each Flow Type
Laminar flow is governed primarily by the incompressible Navier-Stokes equations, which assume constant density and focus on viscous shear forces acting within a fluid moving in parallel layers. Compressible flow involves the full compressible Navier-Stokes equations, incorporating variable density, pressure, temperature, and energy conservation to account for changes in fluid properties at high speeds or under significant pressure variations. The governing equations for compressible flow include the continuity equation, momentum equations, and energy equation, all coupled with the equation of state to relate thermodynamic variables.
Real-World Applications of Laminar Flow
Laminar flow, characterized by smooth, orderly fluid motion with minimal mixing, is critical in applications such as aerodynamic design, microfluidic devices, and chemical processing, where precise control over fluid behavior is essential. This flow type reduces drag on aircraft surfaces, enhances heat exchanger efficiency, and improves accuracy in biomedical devices by maintaining stable flow conditions. In contrast, compressible flow involves significant density changes, relevant in high-speed aerodynamics and gas pipelines, highlighting the distinct operational environments of laminar flow.
Practical Uses of Compressible Flow
Compressible flow is essential in the design of high-speed aircraft, rockets, and gas turbines, where changes in density significantly affect performance and efficiency. It plays a critical role in nozzle flow analysis, supersonic wind tunnels, and shockwave formation, enabling precise control of aerodynamic forces. Practical applications also include high-speed ventilation systems and natural gas pipelines, where compressibility impacts pressure and flow rate management.
Transition from Laminar to Compressible Regimes
The transition from laminar to compressible flow occurs when the fluid velocity approaches or exceeds the speed of sound, causing significant changes in density and pressure that disrupt the smooth, orderly laminar motion. In laminar flow, fluid particles move in parallel layers with minimal mixing, but compressible flow introduces shock waves, expansion fans, and density variations that result in turbulence and complex flow patterns. Key parameters influencing this transition include the Mach number, Reynolds number, and temperature gradients, which collectively determine when flow regime shifts from incompressible laminar to compressible turbulent behavior.
Challenges in Modeling Both Flows
Modeling laminar flow requires precise resolution of viscous effects at low Reynolds numbers to accurately capture smooth, orderly fluid motion. Compressible flow modeling faces challenges in accounting for density variations, shock waves, and rapid changes in pressure and temperature within high-speed environments. Both demand specialized numerical methods and turbulence models to ensure stability and accuracy in simulations under varying fluid dynamic conditions.
Summary and Future Trends in Fluid Dynamics
Laminar flow, characterized by smooth, orderly fluid motion, contrasts with compressible flow, which involves significant density changes due to pressure variations. Advances in computational fluid dynamics (CFD) enable precise modeling of complex laminar-to-turbulent transitions and compressible shockwave interactions, enhancing aerospace and automotive design. Future trends emphasize machine learning integration and high-fidelity simulations to optimize flow control, energy efficiency, and noise reduction in both laminar and compressible flow regimes.
Laminar flow Infographic
 libterm.com
libterm.com