Hydrostatic stress refers to the uniform pressure applied equally in all directions within a material, influencing its volume without causing shape distortion. It plays a crucial role in material science and engineering, affecting phenomena such as phase transformations, fracture behavior, and fluid flow. Explore the rest of the article to understand how hydrostatic stress impacts your applications and materials.
Table of Comparison
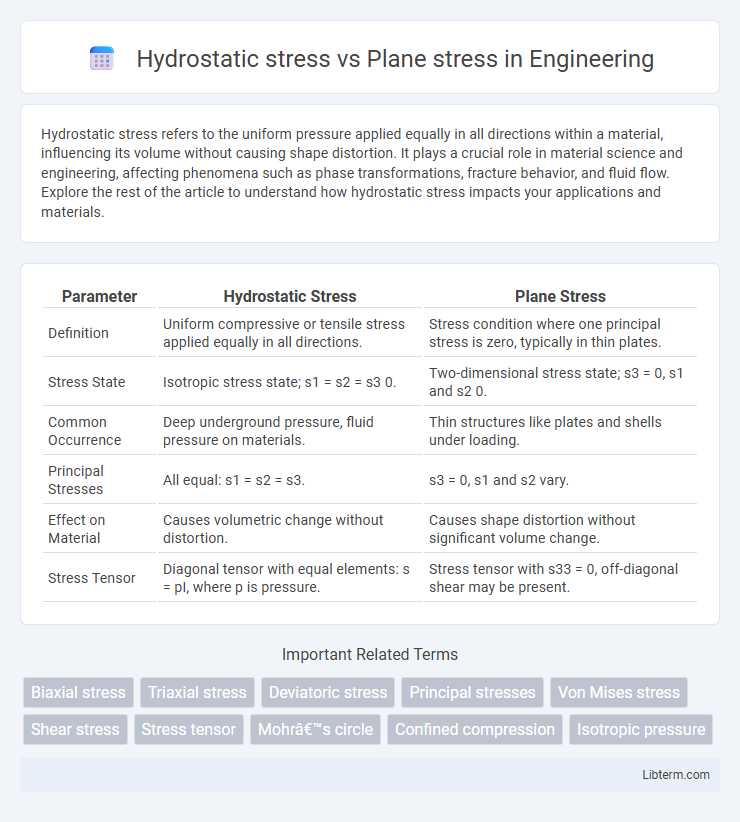
| Parameter | Hydrostatic Stress | Plane Stress |
|---|---|---|
| Definition | Uniform compressive or tensile stress applied equally in all directions. | Stress condition where one principal stress is zero, typically in thin plates. |
| Stress State | Isotropic stress state; s1 = s2 = s3 0. | Two-dimensional stress state; s3 = 0, s1 and s2 0. |
| Common Occurrence | Deep underground pressure, fluid pressure on materials. | Thin structures like plates and shells under loading. |
| Principal Stresses | All equal: s1 = s2 = s3. | s3 = 0, s1 and s2 vary. |
| Effect on Material | Causes volumetric change without distortion. | Causes shape distortion without significant volume change. |
| Stress Tensor | Diagonal tensor with equal elements: s = pI, where p is pressure. | Stress tensor with s33 = 0, off-diagonal shear may be present. |
Introduction to Stress in Materials
Hydrostatic stress refers to the uniform pressure applied equally in all directions within a material, significantly influencing volumetric changes without causing distortion. Plane stress occurs in thin structures where stress is assumed to be zero across the thickness, affecting only the in-plane components of the stress tensor. Understanding these fundamental stress states is crucial for analyzing material behavior, failure mechanisms, and designing components subjected to different loading conditions.
Defining Hydrostatic Stress
Hydrostatic stress is defined as the isotropic part of the stress tensor where normal stresses are equal in all directions, resulting in uniform pressure without shear components. It represents a state of stress that changes volume but does not cause distortion, crucial in analyzing fluid pressure and material behavior under compression. Unlike plane stress, which assumes zero stress in the thickness direction, hydrostatic stress fully accounts for tridimensional normal stress components equally applied.
Defining Plane Stress
Plane stress is a state in which stress components perpendicular to a specific plane are assumed to be zero, typically occurring in thin structures where out-of-plane stresses are negligible. Hydrostatic stress represents an equal magnitude of normal stress applied uniformly in all directions, leading to volumetric changes without shape distortion. Plane stress simplifies analysis by focusing on in-plane stresses, excluding hydrostatic components that affect three-dimensional stress states.
Key Differences Between Hydrostatic and Plane Stress
Hydrostatic stress involves equal magnitude of stress applied uniformly in all directions, resulting in volumetric changes without shape distortion, whereas plane stress occurs when stress acts primarily in two dimensions with negligible stress in the third, typically in thin structures. Hydrostatic stress is characterized by a mean normal stress that affects material volume, while plane stress focuses on in-plane stresses influencing shape and structural integrity. Understanding these differences is crucial for material failure analysis and design in fields like geomechanics and aerospace engineering.
Mathematical Representation of Hydrostatic Stress
Hydrostatic stress is mathematically represented as the average of the normal stresses, expressed as s_h = (s_x + s_y + s_z) / 3, where s_x, s_y, and s_z are the principal stresses in three orthogonal directions. This scalar quantity signifies uniform compression or tension without shear components, contrasting with plane stress, which considers only two dimensions, typically s_x and s_y, with s_z assumed zero. Hydrostatic stress plays a critical role in yielding criteria and material behavior under tri-axial loading conditions.
Mathematical Representation of Plane Stress
Plane stress assumes stress components perpendicular to the plane are zero, represented mathematically as s_z = t_xz = t_yz = 0. The state of stress is defined only by s_x, s_y, and t_xy, simplifying the 3D stress tensor into a 2D form for thin plates or shells. This assumption facilitates solving complex elasticity problems by reducing the stress tensor to a 2x2 matrix, optimizing computational efficiency in structural analysis.
Real-World Examples and Applications
Hydrostatic stress plays a critical role in deep-sea engineering and geotechnical applications, where uniform pressure impacts materials and structures underwater or underground. Plane stress conditions are prevalent in thin-walled components such as aircraft fuselages and automotive panels, where stress is primarily distributed in two dimensions due to negligible thickness. Understanding the differences helps engineers optimize designs for safety and performance in scenarios ranging from pipeline integrity under high pressure to thin film materials in electronics.
Effects on Material Behavior
Hydrostatic stress induces uniform volumetric changes in materials without causing shape distortion, significantly influencing phenomena such as void nucleation and growth leading to ductile fracture. Plane stress conditions constrain stress to two dimensions, promoting localized plastic deformation and shear band formation, which affect the material's yield and failure modes. Understanding these differing stress states allows engineers to predict material response under complex loading scenarios, crucial for designing components subjected to varying stress environments.
Importance in Engineering and Design
Hydrostatic stress and plane stress are critical concepts in engineering and design due to their distinct effects on material behavior and failure mechanisms. Hydrostatic stress, which acts equally in all directions, significantly influences volumetric changes and material density, playing a vital role in applications involving fluid pressure and bulk material compaction. Plane stress conditions, prevalent in thin structural components, are essential for analyzing stress distributions and predicting yielding or fracture in plates, shells, and thin-walled structures, ensuring safe and efficient design.
Summary and Conclusion
Hydrostatic stress occurs when equal normal stresses are applied uniformly in all directions, resulting in volumetric changes without shape distortion, while plane stress assumes zero stress in the thickness direction and is typically used for thin structures. Hydrostatic stress influences material behavior related to volumetric expansion and pressure-dependent yielding, whereas plane stress facilitates analysis of thin plates and shells under in-plane loads. Understanding the distinction aids in selecting appropriate stress models for accurate structural analysis and material failure predictions.
Hydrostatic stress Infographic
 libterm.com
libterm.com