Voltage ratio defines the relationship between the input and output voltages in electrical circuits, essential for understanding transformers and power distribution. It is a critical parameter in designing systems that require voltage step-up or step-down for efficient energy transfer. Explore the rest of the article to learn how voltage ratio impacts your electrical applications and improve your system's performance.
Table of Comparison
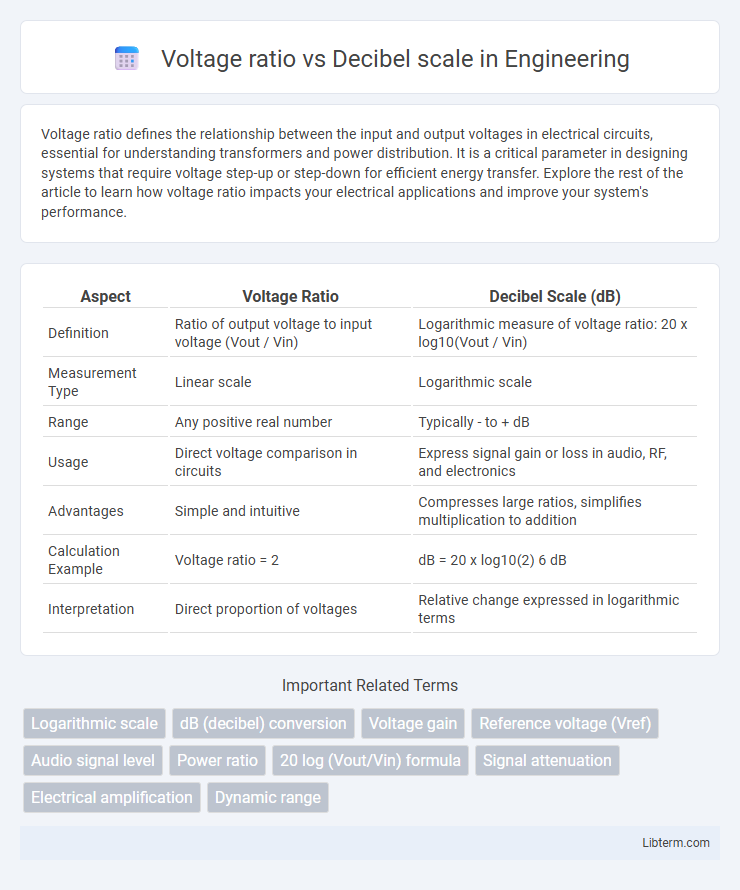
| Aspect | Voltage Ratio | Decibel Scale (dB) |
|---|---|---|
| Definition | Ratio of output voltage to input voltage (Vout / Vin) | Logarithmic measure of voltage ratio: 20 x log10(Vout / Vin) |
| Measurement Type | Linear scale | Logarithmic scale |
| Range | Any positive real number | Typically - to + dB |
| Usage | Direct voltage comparison in circuits | Express signal gain or loss in audio, RF, and electronics |
| Advantages | Simple and intuitive | Compresses large ratios, simplifies multiplication to addition |
| Calculation Example | Voltage ratio = 2 | dB = 20 x log10(2) 6 dB |
| Interpretation | Direct proportion of voltages | Relative change expressed in logarithmic terms |
Introduction to Voltage Ratio and Decibel Scale
Voltage ratio quantifies the proportion between two voltage levels, often expressed as a simple ratio or a factor. The decibel (dB) scale provides a logarithmic measurement of this ratio, enabling easier comparison of vastly different voltage values by converting multiplicative changes into additive units. Using the formula 20 log10(Vout/Vin), the decibel scale translates voltage ratios into a standardized, scalable format widely used in electronics and signal processing.
Understanding Voltage Ratio: Definition and Importance
Voltage ratio represents the relationship between two voltage levels, expressed as a simple numerical value indicating how many times one voltage is greater than the other. This ratio is crucial in electronics and signal processing to quantify signal amplification or attenuation precisely. Understanding voltage ratio enables accurate interpretation and comparison of signal strength changes, forming the foundation for converting values into the decibel (dB) scale used widely in audio, telecommunications, and engineering.
What is the Decibel (dB) Scale?
The decibel (dB) scale is a logarithmic unit used to express the ratio between two voltage levels, providing a more manageable way to represent large variations in signal strength. Voltage ratio in decibels is calculated as 20 times the base-10 logarithm of the ratio between two voltage values, reflecting the power relationship where power is proportional to the square of the voltage. This scale simplifies comparisons in electronics and acoustics by compressing wide-ranging voltage ratios into a compact numeric range.
Why Use Decibels to Measure Voltage?
Using decibels (dB) to measure voltage provides a logarithmic scale that simplifies the representation of large voltage variations, making it easier to compare signal levels across a wide dynamic range. The voltage ratio expressed in decibels quantifies relative changes, which aligns with human perception of sound and signal intensity, allowing engineers to analyze and interpret signal gains or losses more effectively. Decibel measurements also facilitate the combination and subtraction of signal levels in complex circuits, improving clarity and precision in electrical engineering applications.
Mathematical Relationship: Voltage Ratio to Decibel Conversion
The mathematical relationship between voltage ratio and decibel scale is defined by the formula \( \text{dB} = 20 \log_{10} \left( \frac{V_2}{V_1} \right) \), where \( V_2 \) and \( V_1 \) represent the output and reference voltages, respectively. This logarithmic conversion expresses the voltage ratio in decibels, facilitating easier comparison and analysis of signal levels. Using this formula, a voltage ratio of 10 corresponds to 20 dB, highlighting the exponential nature of the decibel scale relative to voltage values.
Formula for Calculating Voltage in Decibels
The voltage ratio in decibels (dB) is calculated using the formula \( dB = 20 \log_{10}\left(\frac{V_2}{V_1}\right) \), where \(V_2\) and \(V_1\) represent the output and reference voltages respectively. This logarithmic relation helps convert multiplicative voltage ratios into additive decibel values for easier comparison. The factor of 20 arises because power is proportional to the square of voltage, and decibels are a power ratio measure expressed on a logarithmic scale.
Interpreting Decibel Values in Electrical Engineering
Decibel (dB) values represent voltage ratios logarithmically, calculated as 20 times the base-10 logarithm of the voltage ratio (20 log10(V_out/V_in)). In electrical engineering, this scale simplifies expressing large voltage ranges, enabling easier comparison and analysis of signal strength, gain, or attenuation. Understanding that a 6 dB increase corresponds to doubling voltage, while a -6 dB decrease represents halving, is crucial for interpreting circuit performance and signal integrity.
Practical Examples: Voltage Ratios and Corresponding dB Values
A voltage ratio of 2 corresponds to approximately 6 dB, indicating that the signal amplitude has doubled, while a voltage ratio of 0.5 equates to -6 dB, showing the signal amplitude has halved. In audio engineering, a voltage ratio of 10 results in 20 dB, commonly used to measure gain stages and amplifier output levels. Understanding these relationships aids technicians in accurately converting voltage increases or decreases into decibel values for effective signal processing.
Common Applications of Voltage Ratio and Decibel Scale
Voltage ratio is commonly used in electronic circuit design and signal processing to measure and compare input and output voltage levels, ensuring proper signal amplification and attenuation. The decibel scale is extensively applied in telecommunications, audio engineering, and acoustics for quantifying gain, loss, and signal strength over a logarithmic scale that simplifies the handling of large voltage variations. Both scales are essential in RF engineering for evaluating amplifier performance, impedance matching, and noise figure analysis, enabling precise control and optimization of electronic systems.
Conclusion: Significance of Decibel Scale in Voltage Measurement
The decibel scale provides a logarithmic representation of voltage ratios, enabling easier interpretation of large variations in signal strength. Its ability to convert multiplicative voltage changes into additive decibel values simplifies comparison and analysis of electrical signals. This scale is essential in voltage measurement for precise communication of gain or loss across systems, especially in audio, radio frequency, and telecommunications engineering.
Voltage ratio Infographic
 libterm.com
libterm.com