Analytical methods encompass a variety of techniques used to identify, quantify, and understand the components and structure of substances in scientific research and industry. These methods range from chromatography and spectroscopy to titration and mass spectrometry, each providing unique insights into material composition and behavior. Explore this article to discover how these powerful tools can enhance your precision and reliability in analysis.
Table of Comparison
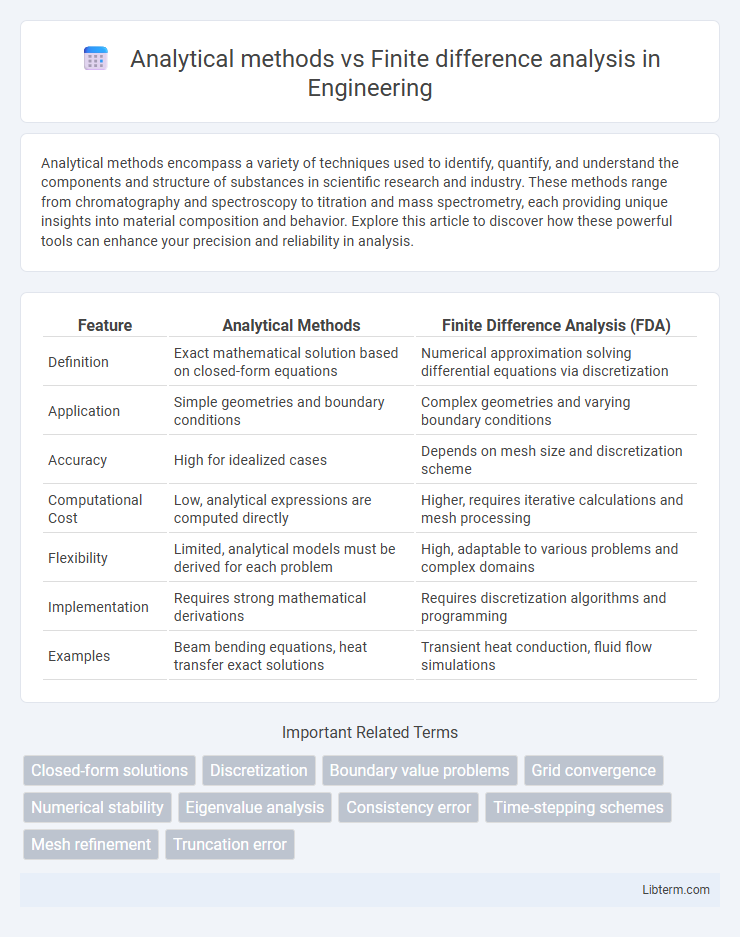
| Feature | Analytical Methods | Finite Difference Analysis (FDA) |
|---|---|---|
| Definition | Exact mathematical solution based on closed-form equations | Numerical approximation solving differential equations via discretization |
| Application | Simple geometries and boundary conditions | Complex geometries and varying boundary conditions |
| Accuracy | High for idealized cases | Depends on mesh size and discretization scheme |
| Computational Cost | Low, analytical expressions are computed directly | Higher, requires iterative calculations and mesh processing |
| Flexibility | Limited, analytical models must be derived for each problem | High, adaptable to various problems and complex domains |
| Implementation | Requires strong mathematical derivations | Requires discretization algorithms and programming |
| Examples | Beam bending equations, heat transfer exact solutions | Transient heat conduction, fluid flow simulations |
Introduction to Analytical Methods and Finite Difference Analysis
Analytical methods provide exact solutions to differential equations by applying algebraic manipulations and calculus, commonly used in simpler, well-defined problems. Finite difference analysis approximates solutions by discretizing continuous domains into grid points, enabling numerical solutions to complex differential equations where analytical methods fall short. This numerical approach, based on finite difference equations, is widely utilized in engineering fields for structural analysis, heat transfer, and fluid dynamics simulations.
Fundamental Principles of Analytical Methods
Analytical methods rely on closed-form mathematical expressions derived from fundamental physical laws such as differential equations, enabling exact solutions that describe system behavior under idealized conditions. These methods utilize principles like linearity, superposition, and boundary conditions to solve problems involving heat transfer, fluid flow, or structural analysis without numerical approximations. Finite difference analysis, by contrast, discretizes these governing equations over a mesh or grid to obtain approximate numerical solutions where analytical methods become intractable.
Core Concepts in Finite Difference Analysis
Finite difference analysis approximates solutions to differential equations by discretizing continuous domains into grids, enabling numerical estimation of derivatives through difference equations. Core concepts include mesh generation for spatial and temporal discretization, stability criteria to ensure convergence, and accurate representation of boundary conditions. Unlike analytical methods that yield exact formulas, finite difference analysis provides flexible, approximate solutions for complex problems in engineering and physical sciences.
Mathematical Formulation Differences
Analytical methods rely on exact mathematical expressions derived from fundamental equations such as differential equations, allowing precise solutions under idealized conditions. Finite difference analysis approximates these equations by discretizing the domain into a grid and replacing derivatives with difference equations, enabling numerical solutions for complex geometries and boundary conditions. The key mathematical distinction lies in analytical methods solving continuous functions explicitly, whereas finite difference uses discrete approximations to iteratively approach the solution.
Applications in Engineering and Science
Analytical methods provide exact solutions for engineering and scientific problems, especially in structural analysis, fluid dynamics, and thermal systems, enabling precise modeling of idealized scenarios. Finite difference analysis offers numerical approximations for complex systems where analytical solutions are impractical, commonly used in heat transfer simulations, wave propagation, and stress-strain evaluations in heterogeneous materials. The choice depends on problem complexity, with analytical methods favored for simpler, linear models and finite difference techniques preferred for large-scale, nonlinear, or time-dependent applications.
Advantages of Analytical Methods
Analytical methods provide exact solutions for engineering and scientific problems by solving differential equations symbolically, ensuring high accuracy and clarity in understanding fundamental behaviors. These methods enable quick evaluations without the need for extensive computational resources or discretization errors inherent in finite difference analysis. Analytical solutions also facilitate parametric studies and sensitivity analyses, offering clear insights into system dependencies and guiding design optimization efficiently.
Benefits of Finite Difference Analysis
Finite difference analysis offers enhanced flexibility in solving complex differential equations that are difficult or impossible to address analytically, enabling accurate modeling of irregular geometries and boundary conditions. It allows for numerical approximation of solutions over discrete grids, facilitating the simulation of dynamic systems and transient phenomena with high precision. This method supports iterative refinement and adaptation, improving solution accuracy and enabling practical application to a wide range of engineering and scientific problems.
Limitations and Challenges of Each Approach
Analytical methods for solving differential equations provide exact solutions but are limited to simple geometries and boundary conditions, making them impractical for complex real-world problems. Finite difference analysis, on the other hand, offers numerical approximations capable of handling complex domains and irregular geometries but faces challenges such as discretization errors, convergence issues, and the need for extensive computational resources. Both approaches require careful consideration of problem-specific parameters to ensure accuracy and stability, with analytical methods restricted by their assumptions and finite difference methods dependent on mesh quality and numerical stability criteria.
Case Studies and Comparative Examples
Case studies reveal that analytical methods provide exact solutions for simple geometries and boundary conditions, offering clarity in stress and deformation predictions. Finite difference analysis excels in handling complex, real-world problems with irregular geometries and nonlinear materials, demonstrated through comparative examples in structural engineering and heat transfer simulations. Comparative studies highlight trade-offs in accuracy, computational cost, and adaptability, guiding engineers in method selection based on project-specific requirements.
Choosing the Right Method for Your Problem
Analytical methods provide exact solutions for problems with simplified geometries and boundary conditions, making them ideal for initial design and validation phases. Finite difference analysis excels in handling complex, nonlinear problems and irregular domains by discretizing equations for numerical approximation. Selecting the right method depends on problem complexity, required accuracy, computational resources, and the nature of the physical phenomena involved.
Analytical methods Infographic
 libterm.com
libterm.com