Meshfree methods offer a flexible and efficient approach for solving complex engineering problems without relying on traditional mesh generation, enhancing computational accuracy and adaptability. These techniques are particularly useful for simulations involving large deformations, fractures, and other nonlinear phenomena where mesh-based methods struggle. Explore this article to discover how meshfree methods can transform your computational modeling processes.
Table of Comparison
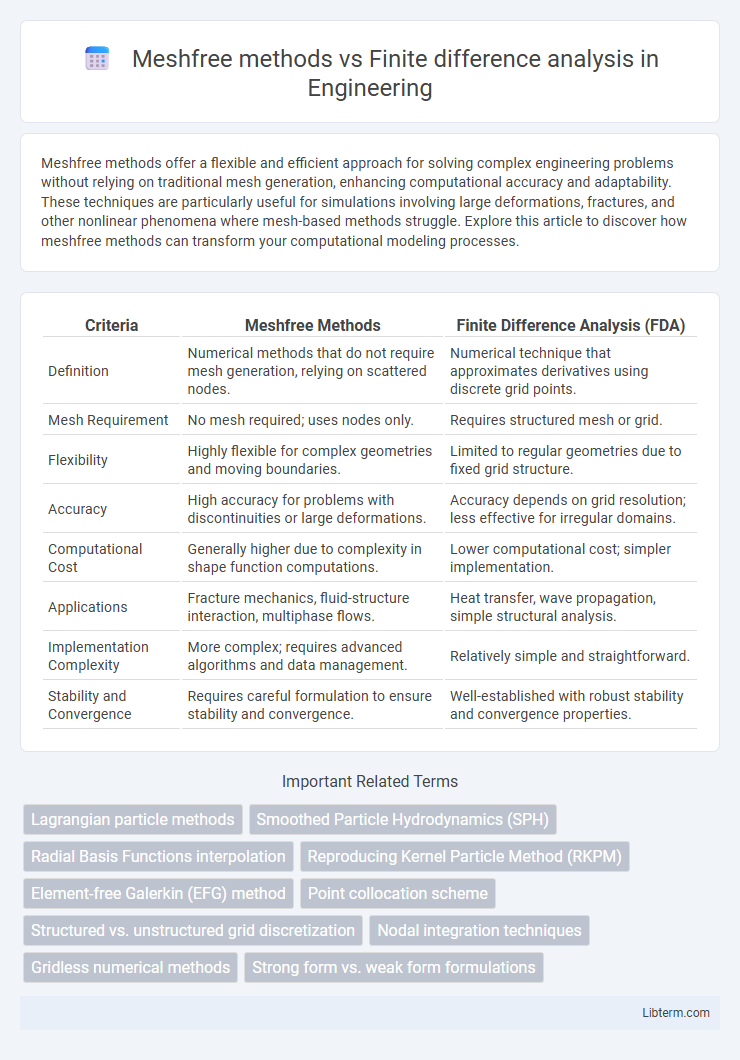
| Criteria | Meshfree Methods | Finite Difference Analysis (FDA) |
|---|---|---|
| Definition | Numerical methods that do not require mesh generation, relying on scattered nodes. | Numerical technique that approximates derivatives using discrete grid points. |
| Mesh Requirement | No mesh required; uses nodes only. | Requires structured mesh or grid. |
| Flexibility | Highly flexible for complex geometries and moving boundaries. | Limited to regular geometries due to fixed grid structure. |
| Accuracy | High accuracy for problems with discontinuities or large deformations. | Accuracy depends on grid resolution; less effective for irregular domains. |
| Computational Cost | Generally higher due to complexity in shape function computations. | Lower computational cost; simpler implementation. |
| Applications | Fracture mechanics, fluid-structure interaction, multiphase flows. | Heat transfer, wave propagation, simple structural analysis. |
| Implementation Complexity | More complex; requires advanced algorithms and data management. | Relatively simple and straightforward. |
| Stability and Convergence | Requires careful formulation to ensure stability and convergence. | Well-established with robust stability and convergence properties. |
Introduction to Numerical Analysis Methods
Meshfree methods offer enhanced flexibility in solving partial differential equations by eliminating the need for predefined mesh grids, contrasting with the structured grid dependency inherent in finite difference analysis. Finite difference analysis relies on discretizing the domain into a fixed grid, using difference equations to approximate derivatives and solve problems numerically, which can struggle with complex geometries or boundary conditions. In numerical analysis, meshfree techniques facilitate adaptability and accuracy for problems involving large deformations or moving boundaries, making them increasingly advantageous over traditional finite difference methods in certain engineering and physics simulations.
Overview of Meshfree Methods
Meshfree methods are numerical techniques used for solving partial differential equations without relying on a predefined mesh, which enhances flexibility in handling complex geometries and large deformations. These methods, such as Smoothed Particle Hydrodynamics (SPH) and Element-Free Galerkin (EFG), approximate solutions using scattered nodes, enabling improved accuracy near discontinuities and free surfaces. Unlike finite difference analysis that requires structured grids, meshfree methods inherently adapt to evolving domains, making them highly suitable for fluid dynamics, fracture mechanics, and multiphysics simulations.
Fundamentals of Finite Difference Analysis
Finite difference analysis relies on discretizing a domain into a structured grid where differential equations are approximated using differences between function values at grid points, enabling numerical solutions of partial differential equations. The method's accuracy depends on grid resolution and the order of finite difference approximations, with central differences providing higher accuracy for derivatives. Unlike meshfree methods that use point clouds without structured meshes, finite difference analysis requires a predefined mesh, which can limit flexibility but simplifies the formulation for problems with regular geometries.
Key Theoretical Differences
Meshfree methods eliminate the need for predefined grids by utilizing scattered nodes and shape functions for spatial discretization, enabling greater flexibility in modeling complex geometries and large deformations. Finite difference analysis relies on structured grids and finite difference equations to approximate derivatives at discrete points, which can limit adaptability in irregular domains. Unlike finite difference methods, meshfree techniques inherently support higher-order continuity and smooth approximations through kernel functions and moving least squares approximations, enhancing accuracy in problems involving discontinuities or evolving boundaries.
Accuracy and Convergence Comparison
Meshfree methods demonstrate higher accuracy in handling complex geometries and discontinuities due to their flexibility in node distribution, unlike finite difference analysis which relies on fixed grid structures prone to interpolation errors. Convergence rates of meshfree methods often surpass finite difference schemes, especially in problems with irregular domains or moving boundaries, as they avoid the dependency on structured meshes. However, finite difference analysis generally benefits from simpler implementation and well-established convergence proofs for smooth problems with regular grids.
Computational Efficiency and Scalability
Meshfree methods offer superior scalability compared to finite difference analysis (FDA) by eliminating the need for structured grids, enabling efficient handling of complex geometries and large deformations. FDA relies on fixed grid discretization, which can lead to computational bottlenecks and reduced efficiency as problem size increases. Meshfree techniques leverage scattered nodes and adaptive refinement, resulting in improved computational efficiency for high-dimensional and nonlinear problems.
Flexibility in Complex Geometries
Meshfree methods offer superior flexibility in handling complex geometries due to their node-based formulation, eliminating the need for mesh generation that often struggles with irregular shapes and discontinuities. Finite difference analysis relies on structured grids, making it less adaptable to intricate boundaries and geometrical complexities without significant grid refinement or transformation techniques. Therefore, meshfree approaches provide enhanced accuracy and computational efficiency when modeling problems involving evolving domains or complex geometrical features.
Application Areas and Use Cases
Meshfree methods excel in complex engineering simulations involving large deformations, fracture mechanics, and fluid-structure interactions where traditional mesh generation is challenging. Finite difference analysis is widely used in solving partial differential equations for heat transfer, fluid dynamics, and wave propagation in structured grid domains with regular geometries. Industries such as aerospace and biomechanics leverage meshfree methods for modeling material failure, while finite difference techniques dominate applications in geophysics and meteorology for weather prediction and seismic analysis.
Limitations and Challenges
Meshfree methods face challenges in computational cost and stability when handling complex boundary conditions compared to Finite Difference Analysis (FDA), which is limited by its dependence on structured grids and difficulty in modeling irregular geometries. FDA struggles with accuracy near discontinuities and complex domains, while meshfree methods require sophisticated algorithms for shape function construction and integration, impacting computational efficiency. Both techniques encounter difficulties in balancing accuracy, convergence, and computational resources for high-dimensional or nonlinear problems.
Future Trends in Numerical Analysis Methods
Meshfree methods are gaining significant traction over finite difference analysis due to their flexibility in handling complex geometries and evolving discontinuities without requiring mesh generation. Emerging trends emphasize integrating machine learning algorithms with meshfree approaches to enhance computational efficiency and accuracy in multi-scale simulations. Research is also focusing on hybrid methods that combine meshfree techniques with traditional finite difference schemes to leverage the strengths of both methods for future numerical analysis challenges.
Meshfree methods Infographic
 libterm.com
libterm.com