Analytical methods play a crucial role in accurately identifying and quantifying substances within a sample, utilizing techniques such as chromatography, spectroscopy, and titration. These methods enhance the precision and reliability of experimental results by providing detailed insights into the chemical composition and properties of materials. Explore the rest of the article to understand how these methods can improve your scientific investigations.
Table of Comparison
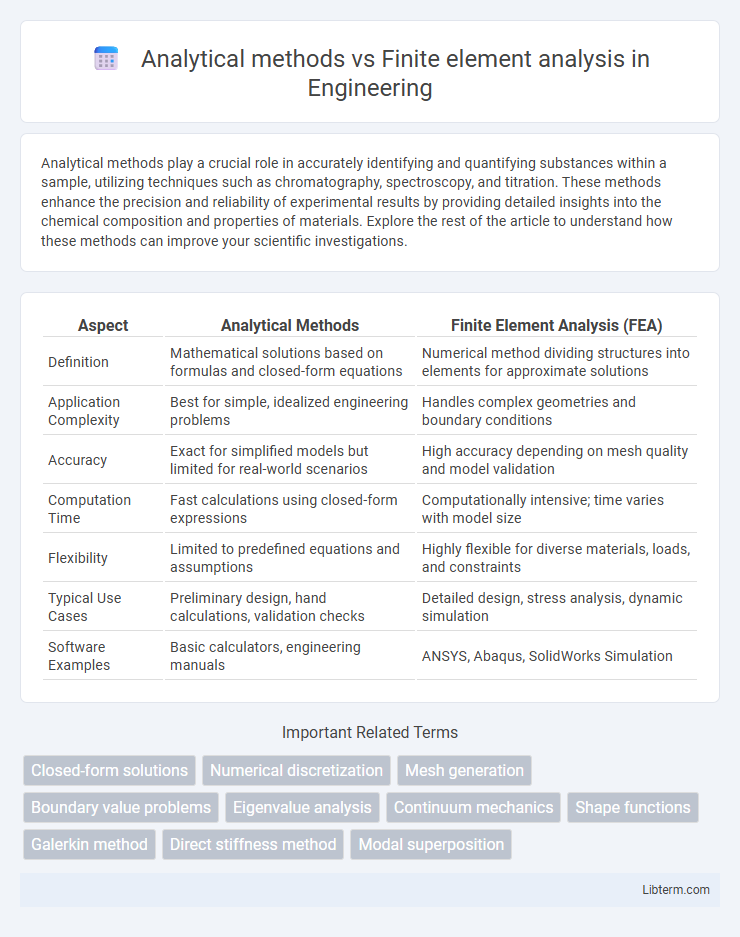
| Aspect | Analytical Methods | Finite Element Analysis (FEA) |
|---|---|---|
| Definition | Mathematical solutions based on formulas and closed-form equations | Numerical method dividing structures into elements for approximate solutions |
| Application Complexity | Best for simple, idealized engineering problems | Handles complex geometries and boundary conditions |
| Accuracy | Exact for simplified models but limited for real-world scenarios | High accuracy depending on mesh quality and model validation |
| Computation Time | Fast calculations using closed-form expressions | Computationally intensive; time varies with model size |
| Flexibility | Limited to predefined equations and assumptions | Highly flexible for diverse materials, loads, and constraints |
| Typical Use Cases | Preliminary design, hand calculations, validation checks | Detailed design, stress analysis, dynamic simulation |
| Software Examples | Basic calculators, engineering manuals | ANSYS, Abaqus, SolidWorks Simulation |
Introduction to Analytical Methods and Finite Element Analysis
Analytical methods rely on exact mathematical equations to solve engineering problems, typically providing closed-form solutions for simpler geometries and loading conditions. Finite Element Analysis (FEA) approximates complex structures by discretizing them into finite elements, enabling numerical solutions where analytical methods are impractical. FEA is widely used for stress, thermal, and dynamic analyses, offering greater flexibility and accuracy for intricate designs and boundary conditions.
Fundamental Principles of Analytical Methods
Analytical methods rely on exact mathematical formulations based on fundamental principles such as equilibrium, compatibility, and constitutive relations to solve engineering problems. These methods use closed-form solutions derived from differential equations and boundary conditions, providing precise and easily interpretable results for simple geometries and loading conditions. Finite element analysis, in contrast, approximates the solution by discretizing the domain into smaller elements, making it suitable for complex structures where analytical methods become impractical.
Core Concepts of Finite Element Analysis
Finite element analysis (FEA) decomposes complex structures into smaller, manageable elements, enabling detailed stress, strain, and displacement calculations that surpass the simplifications of traditional analytical methods. Core concepts of FEA include discretization, element formulation, shape functions, and assembly of the global stiffness matrix, which collectively transform differential equations into solvable algebraic forms. This approach allows engineers to model intricate geometries and boundary conditions with higher accuracy, facilitating predictive simulations in structural, thermal, and fluid dynamics problems.
Advantages of Analytical Methods
Analytical methods offer precise, exact solutions for simpler engineering problems, enabling rapid calculations with minimal computational resources. They provide clear insight into the relationships between variables, facilitating easier error detection and validation of results. These methods excel in problems with well-defined boundary conditions, making them ideal for initial design stages and theoretical validation compared to the complexity of Finite Element Analysis (FEA).
Advantages of Finite Element Analysis
Finite Element Analysis (FEA) offers superior versatility in handling complex geometries, material properties, and boundary conditions compared to traditional analytical methods. It enables detailed visualization of stress distribution, deformation, and thermal effects, which are often unattainable through closed-form solutions. FEA's ability to model nonlinear behavior and intricate structures provides precise and practical results for engineering design and optimization.
Limitations of Analytical Methods
Analytical methods for solving engineering problems rely on exact mathematical expressions, which often restrict their applicability to simple geometries and linear material behavior, limiting accuracy in complex structures. These methods struggle with non-linearities, irregular boundary conditions, and multi-scale phenomena that finite element analysis (FEA) can handle more effectively. As a result, analytical approaches are insufficient for modeling real-world applications requiring detailed stress, strain, and deformation analysis in heterogeneous materials and intricate geometries.
Limitations of Finite Element Analysis
Finite Element Analysis (FEA) faces limitations such as high computational cost and increased complexity when modeling non-linear material behavior or large deformations compared to traditional analytical methods. It requires significant expertise to develop accurate mesh quality and boundary conditions, and errors in these inputs can lead to unreliable results. Analytical methods offer closed-form solutions with less computational demand but lack the flexibility to handle complex geometries and real-world conditions that FEA can simulate.
Comparative Applications in Engineering Problems
Analytical methods provide exact solutions for simplified engineering problems with idealized boundary conditions, often used in beam theory and basic heat transfer calculations. Finite element analysis (FEA) excels in complex geometries and non-linear material behaviors, enabling detailed simulations of stress distribution, thermal gradients, and fluid flow in real-world engineering components. Comparing applications, analytical methods suit preliminary design and validation, while FEA supports detailed structural analysis, optimization, and failure prediction in aerospace, automotive, and civil engineering projects.
Selection Criteria: When to Use Analytical Methods vs FEA
Analytical methods are best suited for simple geometries and linear problems where closed-form solutions provide quick and accurate results, such as in basic beam bending or torsion calculations. Finite Element Analysis (FEA) is preferred for complex geometries, nonlinear materials, and boundary conditions requiring detailed stress, strain, and deformation analysis across multiple dimensions. Selection between these methods depends on factors like problem complexity, required accuracy, computational resources, and the ability to model real-world conditions effectively.
Future Trends in Analytical and Numerical Analysis
Emerging trends in analytical methods emphasize integration with machine learning algorithms to enhance prediction accuracy for complex engineering problems. Finite element analysis (FEA) is advancing through the adoption of high-performance computing and adaptive mesh refinement techniques, enabling real-time simulations with increased precision. The convergence of hybrid analytical-numerical approaches is driving innovations in multiphysics modeling, optimizing computational efficiency while maintaining robust solution fidelity.
Analytical methods Infographic
 libterm.com
libterm.com