Free oscillation refers to the natural vibration of a system when it is displaced from its equilibrium position and allowed to oscillate without external forces acting on it. The frequency and amplitude of these oscillations depend on the system's inherent properties like mass and stiffness. Discover how free oscillation affects your understanding of mechanical and electrical systems by reading further.
Table of Comparison
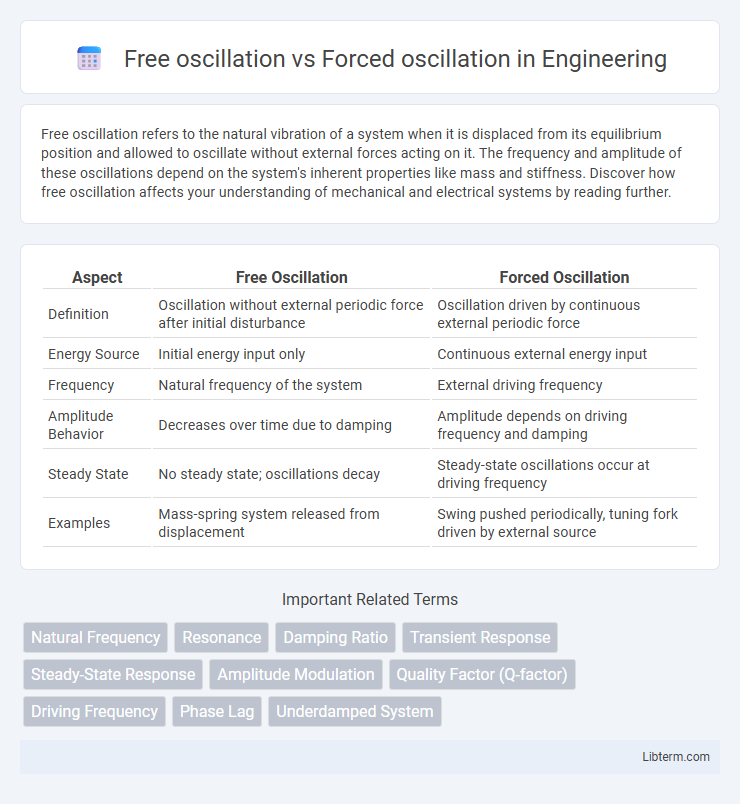
| Aspect | Free Oscillation | Forced Oscillation |
|---|---|---|
| Definition | Oscillation without external periodic force after initial disturbance | Oscillation driven by continuous external periodic force |
| Energy Source | Initial energy input only | Continuous external energy input |
| Frequency | Natural frequency of the system | External driving frequency |
| Amplitude Behavior | Decreases over time due to damping | Amplitude depends on driving frequency and damping |
| Steady State | No steady state; oscillations decay | Steady-state oscillations occur at driving frequency |
| Examples | Mass-spring system released from displacement | Swing pushed periodically, tuning fork driven by external source |
Introduction to Oscillations
Oscillations describe repetitive variations around an equilibrium point, fundamental to understanding mechanical, electrical, and biological systems. Free oscillation occurs when a system moves under the influence of its internal restoring forces without external driving forces, exemplified by a pendulum swinging after being released. Forced oscillation happens when an external periodic force drives the system, causing vibrations at the driving frequency, commonly observed in systems like bridges responding to rhythmic loads or electrical circuits under alternating current.
Defining Free Oscillation
Free oscillation occurs when a system vibrates naturally after being disturbed, without continuous external force. The motion depends solely on the system's inherent properties, such as mass, stiffness, and damping. This contrasts with forced oscillation, where an external periodic force drives the system's vibration.
Understanding Forced Oscillation
Forced oscillation occurs when an external periodic force drives a system, causing it to oscillate at the frequency of the applied force rather than its natural frequency. This phenomenon is critical in engineering and physics, as it influences resonance, where the amplitude of oscillation can dramatically increase if the driving frequency matches the system's natural frequency. Understanding forced oscillation helps in designing structures and systems that can withstand or exploit these vibrations for optimal performance and safety.
Key Differences Between Free and Forced Oscillation
Free oscillation occurs when a system vibrates naturally without external forces after an initial disturbance, characterized by constant amplitude and frequency determined by the system's properties. Forced oscillation happens when an external periodic force drives the system, causing oscillations at the frequency of the driving force, which can lead to resonance if this frequency matches the system's natural frequency. Key differences include energy input, with free oscillations decaying over time due to damping, whereas forced oscillations maintain energy input resulting in sustained or amplified oscillations.
Equation of Motion for Free Oscillation
The equation of motion for free oscillation, \( m\ddot{x} + kx = 0 \), describes a system with mass \( m \) and spring constant \( k \) oscillating without external forces. Solutions to this differential equation yield natural frequency \( \omega_n = \sqrt{k/m} \) and harmonic motion characterized by amplitude and phase constants. Free oscillation analysis is fundamental for understanding undamped mechanical vibrations before introducing forcing functions in forced oscillation scenarios.
Equation of Motion for Forced Oscillation
The equation of motion for forced oscillation is typically expressed as m(d2x/dt2) + c(dx/dt) + kx = F0cos(ot), where m represents mass, c the damping coefficient, k the spring constant, and F0cos(ot) the external periodic force with angular frequency o. In contrast to free oscillation, which occurs without external forces and follows the homogeneous equation m(d2x/dt2) + c(dx/dt) + kx = 0, forced oscillation involves continuous energy input sustaining the system's motion. Solutions to the forced oscillation equation reveal phenomena such as resonance, amplitude versus frequency response, and steady-state oscillatory behavior critical for engineering applications.
Examples of Free Oscillation in Daily Life
A swinging pendulum in a clock and a guitar string vibrating after being plucked are classic examples of free oscillation, where the system vibrates at its natural frequency without continuous external force. Another daily occurrence is the motion of a child on a swing, which gradually slows down due to friction and air resistance but initially moves freely after being pushed. These instances demonstrate how objects oscillate naturally after an initial disturbance, contrasting forced oscillations that require ongoing external energy input.
Real-World Applications of Forced Oscillation
Forced oscillations are crucial in engineering for designing vibration isolation systems in buildings and vehicles to mitigate damage from external periodic forces like earthquakes or engine operation. In mechanical and electrical systems, forced oscillations enable resonance tuning, enhancing the performance of devices such as radio receivers and sensors. Understanding forced oscillations also aids in controlling structural responses in bridges and aircraft wings, preventing catastrophic failures through active damping techniques.
Resonance Effect in Forced Oscillation
Forced oscillation occurs when an external periodic force drives a system, causing it to oscillate at the force's frequency, and resonance arises if this frequency matches the system's natural frequency, leading to a significant increase in amplitude. The resonance effect in forced oscillation can cause large energy buildup and potential structural damage if damping is insufficient. Understanding resonance is critical in engineering designs to prevent catastrophic failures in bridges, buildings, and mechanical systems.
Summary: Choosing Between Free and Forced Oscillation
Free oscillation occurs when a system vibrates at its natural frequency without external influence, ideal for analyzing inherent properties like damping and resonance. Forced oscillation happens when an external periodic force drives the system, allowing precise control over amplitude and frequency for applications such as tuning and vibration testing. Selecting between free and forced oscillation depends on whether the goal is to observe natural system behavior or to control system response under specific external conditions.
Free oscillation Infographic
 libterm.com
libterm.com