Adhesive contact involves the bonding between two surfaces through molecular attractions, creating strong adhesion at the interface. This phenomenon plays a crucial role in industries ranging from electronics to automotive manufacturing, affecting performance and durability. Explore the article to understand how adhesive contact influences your applications and how to optimize it.
Table of Comparison
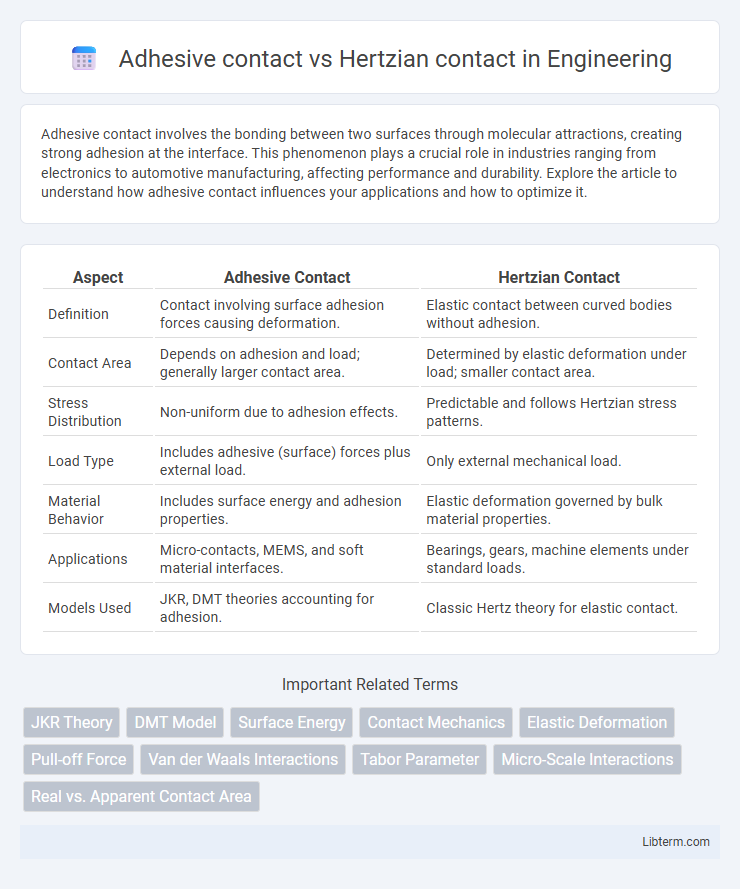
| Aspect | Adhesive Contact | Hertzian Contact |
|---|---|---|
| Definition | Contact involving surface adhesion forces causing deformation. | Elastic contact between curved bodies without adhesion. |
| Contact Area | Depends on adhesion and load; generally larger contact area. | Determined by elastic deformation under load; smaller contact area. |
| Stress Distribution | Non-uniform due to adhesion effects. | Predictable and follows Hertzian stress patterns. |
| Load Type | Includes adhesive (surface) forces plus external load. | Only external mechanical load. |
| Material Behavior | Includes surface energy and adhesion properties. | Elastic deformation governed by bulk material properties. |
| Applications | Micro-contacts, MEMS, and soft material interfaces. | Bearings, gears, machine elements under standard loads. |
| Models Used | JKR, DMT theories accounting for adhesion. | Classic Hertz theory for elastic contact. |
Introduction to Contact Mechanics
Adhesive contact involves surface forces causing materials to stick together at the interface, significantly affecting the contact area and stress distribution. Hertzian contact theory describes the elastic deformation and stress in non-adhesive, frictionless contact between curved surfaces, predicting contact size and pressure without accounting for surface energy effects. Understanding both adhesive and Hertzian contact models is crucial for accurately analyzing real-world interactions in contact mechanics, especially in micro- and nanoscale applications.
Overview of Adhesive Contact Theory
Adhesive contact theory models the interaction between elastic bodies incorporating surface energy effects, contrasting with the purely elastic Hertzian contact which neglects adhesion. It accounts for the attractive forces at the interface, significantly influencing contact area, load distribution, and deformation under small-scale contacts. Models such as the Johnson-Kendall-Roberts (JKR) and Derjaguin-Muller-Toporov (DMT) frameworks describe adhesive contacts, incorporating surface energy parameters alongside elastic moduli.
Fundamentals of Hertzian Contact Theory
Hertzian contact theory describes the stress distribution and deformation occurring when two curved elastic bodies come into contact without adhesion, emphasizing the elastic contact area, contact pressure, and subsurface stress fields. The fundamental equations quantify contact radius, maximum pressure, and deformation based on material properties such as elastic modulus and Poisson's ratio, along with geometric parameters like radius of curvature. This contrasts with adhesive contact models, which incorporate surface energy and intermolecular forces, whereas Hertzian contact strictly assumes frictionless, non-adhesive interactions with purely elastic deformation.
Key Differences Between Adhesive and Hertzian Contact
Adhesive contact involves surface forces causing attraction and potential bonding between contacting bodies, while Hertzian contact refers to elastic deformation under load without surface adhesion. In Hertzian contact, stress distribution is determined by elastic theory and typically results in localized pressure with no sticky effects, whereas adhesive contact exhibits surface energy and molecular interactions influencing contact area and friction. The key difference lies in the presence of interfacial adhesion forces in adhesive contact versus purely mechanical deformation in Hertzian contact.
Material Properties Impacting Contact Behavior
Material properties such as elastic modulus, surface energy, and yield strength critically influence the behavior of adhesive and Hertzian contacts. In adhesive contact, higher surface energy promotes stronger molecular attraction leading to increased adhesion forces, while elasticity determines the extent of real contact area and deformation. Hertzian contact predominantly depends on elastic modulus and hardness, where stiffer materials exhibit smaller contact areas and higher localized stresses, minimizing deformation and adhesion effects.
Role of Surface Roughness in Contact Models
Surface roughness significantly influences both adhesive and Hertzian contact models by affecting the real area of contact and stress distribution between surfaces. In adhesive contact, micro-scale asperities increase surface energy interactions, enhancing adhesion forces, while roughness can reduce intimate contact in Hertzian models, altering load-bearing capacity and contact stiffness. Accurate modeling of surface topography is essential to predict contact mechanics reliably in applications like microelectromechanical systems (MEMS) and tribology.
Applications of Adhesive Contact in Engineering
Adhesive contact plays a critical role in microelectromechanical systems (MEMS) and biomedical devices by enabling strong surface bonding without the need for external fastening methods, improving device miniaturization and reliability. In the design of soft robotics and wearable sensors, adhesive contact mechanisms facilitate reversible attachment and controlled friction, enhancing performance through compliant material interfaces. These applications leverage the surface energy and molecular interactions characteristic of adhesive contact, contrasting with the purely elastic deformation described by Hertzian contact theory in traditional mechanical components.
Practical Uses of Hertzian Contact Analysis
Hertzian contact analysis is widely applied in the design and evaluation of mechanical components such as gears, bearings, and cam followers, where understanding stress distribution and deformation under load is critical for durability and performance. This method enables engineers to predict contact pressure, optimize material selection, and prevent surface fatigue, enhancing the reliability of rotating and sliding elements. Adhesive contact, by contrast, is less common in large-scale mechanical systems and is primarily relevant in micro- and nanoscale applications where surface forces dominate.
Experimental Methods for Contact Characterization
Experimental methods for characterizing adhesive contact typically involve atomic force microscopy (AFM) and surface force apparatus (SFA) to measure force-displacement curves and quantify adhesion forces at the nanoscale. Hertzian contact experiments focus on macroscopic load-deformation behavior using optical interferometry and strain gauge techniques to map pressure distribution and contact area under elastic deformation. Advanced imaging and micro-indentation tests enhance the accuracy of determining mechanical properties and validate theoretical models for both adhesive and Hertzian contacts.
Future Trends in Contact Mechanics Research
Future trends in contact mechanics research emphasize the integration of adhesive contact models with Hertzian contact theory to improve the accuracy of microscale and nanoscale interface predictions. Advanced computational methods and materials characterization techniques are driving innovations in understanding the transition between adhesive and non-adhesive contact regimes. Research is focusing on the development of multiscale models incorporating surface energy effects, roughness, and deformation to better predict contact behavior in emerging technologies such as flexible electronics and biomedical devices.
Adhesive contact Infographic
 libterm.com
libterm.com