Point contact refers to a precise electrical connection between two conductors, often used in semiconductor devices to create localized contact areas. This technique ensures minimal contact resistance and is vital for high-performance electronic components. Explore the full article to understand how point contact technology enhances your device efficiency.
Table of Comparison
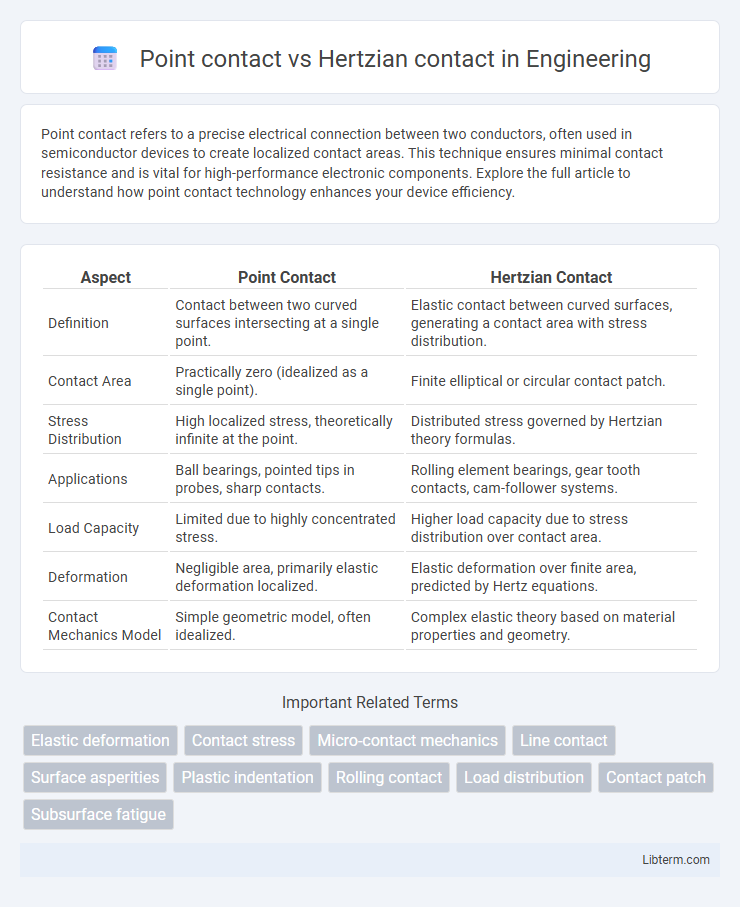
| Aspect | Point Contact | Hertzian Contact |
|---|---|---|
| Definition | Contact between two curved surfaces intersecting at a single point. | Elastic contact between curved surfaces, generating a contact area with stress distribution. |
| Contact Area | Practically zero (idealized as a single point). | Finite elliptical or circular contact patch. |
| Stress Distribution | High localized stress, theoretically infinite at the point. | Distributed stress governed by Hertzian theory formulas. |
| Applications | Ball bearings, pointed tips in probes, sharp contacts. | Rolling element bearings, gear tooth contacts, cam-follower systems. |
| Load Capacity | Limited due to highly concentrated stress. | Higher load capacity due to stress distribution over contact area. |
| Deformation | Negligible area, primarily elastic deformation localized. | Elastic deformation over finite area, predicted by Hertz equations. |
| Contact Mechanics Model | Simple geometric model, often idealized. | Complex elastic theory based on material properties and geometry. |
Introduction to Contact Mechanics
Point contact in contact mechanics refers to the interaction between two curved surfaces, such as spheres or cylinders, where the contact area is initially very small and can be approximated as a single point. Hertzian contact theory provides a mathematical framework to analyze the stress distribution, deformation, and contact area resulting from elastic contact between curved bodies under load. Understanding the distinctions between point contact and Hertzian contact is crucial for predicting material behavior and designing components in mechanical systems subject to localized forces.
Definition of Point Contact
Point contact refers to the interaction between two surfaces where the contact area is theoretically a single point, typically occurring between two spherical or curved bodies. Hertzian contact theory describes the stress distribution, deformation, and size of the contact patch resulting from such point contacts under load. This type of contact is fundamental in analyzing rolling element bearings, gear teeth engagement, and other mechanical components subjected to localized pressure.
Overview of Hertzian Contact
Hertzian contact refers to the stress distribution and deformation that occur when two curved surfaces, such as spheres or cylinders, come into contact under load. This type of contact results in a finite contact area, typically elliptical or circular, where the pressure is highest at the center and decreases towards the edges. Understanding Hertzian contact mechanics is essential in fields like bearing design, gear engineering, and material wear analysis to predict stress, prevent failure, and optimize performance.
Key Differences Between Point and Hertzian Contact
Point contact occurs when two curved surfaces touch at a single point, resulting in highly localized stress, while Hertzian contact refers to the stress distribution generated when two curved bodies press against each other over a small, finite contact area. In point contact, the contact area is theoretically infinitesimal, leading to very high contact stresses, whereas Hertzian contact considers elastic deformation that creates a small elliptical or circular contact patch, reducing peak stresses. The key differences lie in the stress distribution, contact area size, and the inclusion of elastic deformation effects in Hertzian contact versus the idealized point interaction in point contact.
Theoretical Basis of Point Contact
Point contact involves the interaction between two curved surfaces, such as spheres or cylinders, where the contact area is theoretically considered a single point but in practice forms a small elliptical or circular contact patch due to elastic deformation. Hertzian contact theory provides the fundamental mathematical framework for analyzing stresses, contact area, and deformation characteristics under point contact conditions, assuming linear elasticity and frictionless contact between isotropic materials. This theory calculates key parameters like contact radius, maximum pressure, and subsurface stress distributions to predict wear, fatigue, and material behavior in mechanical joints and rolling element bearings.
Principles of Hertzian Contact Theory
Hertzian Contact Theory explains the stress distribution and deformation occurring when two curved surfaces, such as spheres or cylinders, come into contact, producing a contact area rather than a point. In contrast to idealized point contact, which assumes negligible contact area, Hertzian contact considers elastic deformation, resulting in an elliptical or circular contact patch that supports load. Key principles include the calculation of contact pressure, contact area radius, and subsurface stress fields based on material properties and geometry, crucial for analyzing bearing surfaces, gear teeth, and ball contacts.
Applications of Point and Hertzian Contact
Point contact is commonly used in applications involving ball bearings, where the load is transmitted through a small contact area, reducing friction and wear in rotating machinery. Hertzian contact applies in gear tooth interactions and rolling element bearings, where the contact stresses are distributed over elliptical or circular contact areas, ensuring durability under high cyclic loads. Both contact types are critical in automotive suspensions, aerospace joints, and precision machinery for optimizing load-bearing capacity and minimizing surface damage.
Stress Distribution in Contacts
Point contact exhibits highly localized stress distribution characterized by intense compressive stresses concentrated at a singular point, producing elliptical or circular contact areas with steep stress gradients. In Hertzian contact, stress distribution is described by Hertz's equations, showing a semi-elliptical pressure profile that diminishes from the center of the contact patch, resulting in lower peak stresses over a larger area than point contact. Understanding the variation in contact pressure and subsurface stress fields in both contact types is crucial for predicting material deformation and fatigue life in mechanical components.
Advantages and Limitations of Each Approach
Point contact enables high load capacity in compact areas, suitable for applications like ball bearings where minimal friction and localized stress are critical. Hertzian contact distributes stress over a larger contact area, enhancing durability and resistance to wear in components such as gears and cam followers. While point contact offers precise motion control and reduced rolling resistance, it is limited by higher stress concentration and potential fatigue; Hertzian contact provides improved load distribution but may suffer from increased friction and less precise positioning.
Conclusion and Future Perspectives
Point contact typically involves localized stress and deformation at a single or limited number of contact points, leading to higher contact pressure and potential material fatigue. Hertzian contact theory provides a fundamental framework for analyzing elastic contact stresses and deformation in curved surfaces, widely applicable in mechanical and tribological systems. Future research aims to integrate advanced materials and nano-scale surface engineering to enhance contact durability and performance under varying load conditions.
Point contact Infographic
 libterm.com
libterm.com