Plastic contact materials offer excellent electrical conductivity and corrosion resistance, making them ideal for various electronic and industrial applications. Their lightweight and durable properties enhance the efficiency and longevity of devices, ensuring reliable performance under different environmental conditions. Explore the rest of this article to discover how plastic contact materials can improve your projects and applications.
Table of Comparison
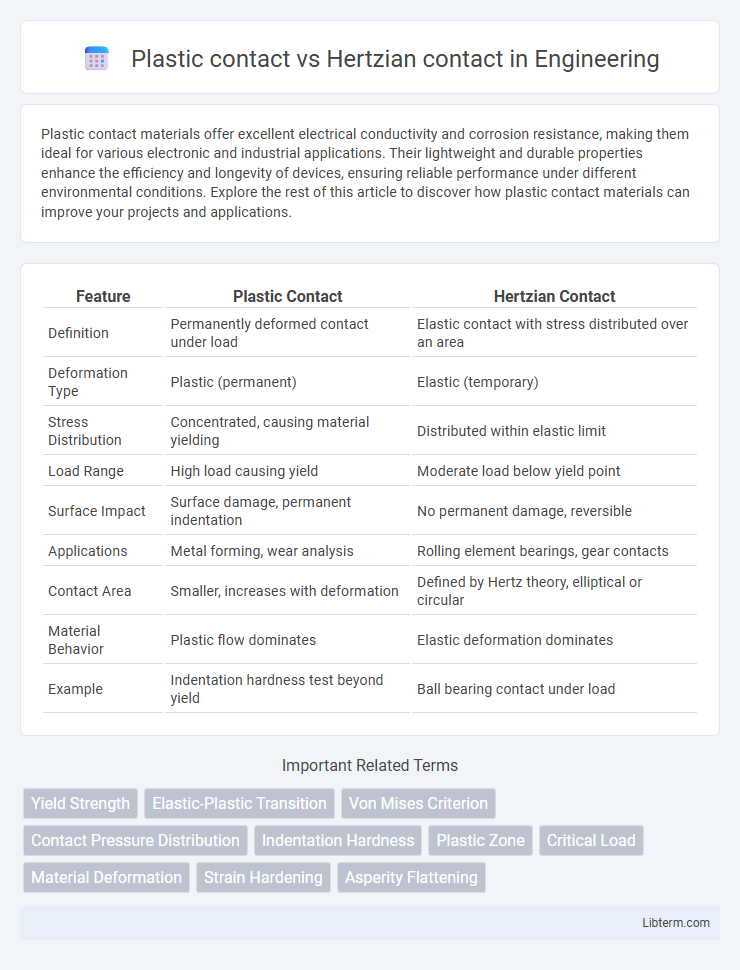
| Feature | Plastic Contact | Hertzian Contact |
|---|---|---|
| Definition | Permanently deformed contact under load | Elastic contact with stress distributed over an area |
| Deformation Type | Plastic (permanent) | Elastic (temporary) |
| Stress Distribution | Concentrated, causing material yielding | Distributed within elastic limit |
| Load Range | High load causing yield | Moderate load below yield point |
| Surface Impact | Surface damage, permanent indentation | No permanent damage, reversible |
| Applications | Metal forming, wear analysis | Rolling element bearings, gear contacts |
| Contact Area | Smaller, increases with deformation | Defined by Hertz theory, elliptical or circular |
| Material Behavior | Plastic flow dominates | Elastic deformation dominates |
| Example | Indentation hardness test beyond yield | Ball bearing contact under load |
Introduction to Contact Mechanics
Plastic contact occurs when the applied load exceeds the yield strength of the material, causing permanent deformation at the interface, while Hertzian contact describes elastic deformation under lower loads where materials return to their original shape. Hertzian contact mechanics is essential for predicting contact stresses and deformation in non-conforming surfaces, such as spheres or cylinders, based on elastic theory developed by Heinrich Hertz. Understanding the transition from elastic to plastic contact allows engineers to design components that avoid failure due to excessive wear or permanent damage.
Defining Plastic Contact and Hertzian Contact
Plastic contact occurs when the applied load exceeds the material yield strength, causing permanent deformation at the contact interface. Hertzian contact involves elastic deformation where stresses remain below the yield point, maintaining reversible contact without permanent shape changes. The Hertzian theory models contact between curved surfaces, predicting contact area and pressure distribution under elastic conditions.
Fundamental Principles of Hertzian Contact Theory
Hertzian contact theory describes the stress distribution and deformation between two elastic bodies in contact, assuming small strains and purely elastic behavior under normal loading. The fundamental principles involve calculating contact area, pressure distribution, and subsurface stress using material properties such as Young's modulus and Poisson's ratio, with contact geometry defined by radii of curvature. Unlike plastic contact, which involves permanent deformation and yield stress, Hertzian contact predicts reversible elastic deformation without material yielding.
Characteristics of Plastic Contact Behavior
Plastic contact behavior occurs when the applied load exceeds the material's yield strength, causing permanent deformation at the contact interface. This results in a large real contact area, increased contact resistance, and altered frictional properties compared to elastic Hertzian contact. The accumulation of plastic strain leads to surface roughening and potential material hardening, significantly affecting wear and fatigue life.
Material Properties Affecting Contact Type
Plastic contact occurs when the applied stress exceeds the material's yield strength, causing permanent deformation, while Hertzian contact involves elastic deformation where stresses remain below the yield point. Material properties such as hardness, yield strength, and elastic modulus critically influence whether a contact behaves plastically or elastically under load. Metals with high yield strength and stiffness typically exhibit Hertzian contact, whereas softer materials with lower yield strength are prone to plastic deformation under comparable stresses.
Mathematical Models of Hertzian and Plastic Contact
Mathematical models of Hertzian contact describe elastic deformation between two curved surfaces, using equations based on Hertz theory to calculate contact stress, contact area, and deformation under load, assuming purely elastic behavior. Plastic contact models incorporate yield criteria such as the von Mises stress and computational approaches like finite element analysis to account for irreversible deformation and material flow beyond the elastic limit. These models often use critical parameters like hardness and yield strength to predict the onset of plasticity, transitioning from Hertzian elastic contact to fully plastic contact conditions under increased loading.
Transition from Elastic (Hertzian) to Plastic Contact
The transition from elastic Hertzian contact to plastic contact occurs when the applied load exceeds the material's yield strength, causing permanent deformation at the contact interface. Hertzian contact theory accurately predicts stress and deformation within the elastic regime, but once plasticity initiates, the contact area grows beyond elastic predictions, lowering contact pressure. Understanding this transition is critical in tribology and material science to optimize surface durability and prevent premature failure in mechanical components.
Applications in Engineering and Technology
Plastic contact is critical in applications involving permanent deformation, such as metal forming, wear analysis, and surface damage prediction in manufacturing processes. Hertzian contact theory applies predominantly to elastic interactions in mechanical systems, including bearing design, gear tooth contact, and lubrication performance in rotating machinery. Engineering solutions leverage plastic contact models for durability assessment, while Hertzian contact models optimize load distribution and stress analysis in high-precision components.
Comparative Analysis: Hertzian vs. Plastic Contacts
Hertzian contact involves elastic deformation where the contact area is small and stress distribution follows a predictable elliptical pattern, commonly analyzed in mechanical components like bearings and gears. Plastic contact occurs when the stress exceeds the material yield strength, causing permanent deformation and increasing the real contact area, which affects wear resistance and fatigue life. Comparative analysis highlights that while Hertzian contact ensures reversible deformation with minimal energy loss, plastic contact leads to irreversible changes, necessitating different design considerations for load capacity and durability.
Challenges and Future Research Directions
Plastic contact involves permanent deformation under load, leading to issues like wear, surface fatigue, and unpredictable material behavior, which complicate accurate modeling and lifespan prediction in engineering applications. Hertzian contact, characterized by elastic deformation and localized stress distribution, faces challenges in addressing deviations from ideal conditions such as surface roughness, material anisotropy, and non-linear elastic responses. Future research aims to develop advanced multi-scale simulation techniques, integrate machine learning for real-time damage prediction, and explore novel materials with enhanced wear resistance to improve reliability and performance of contact mechanics in mechanical systems.
Plastic contact Infographic
 libterm.com
libterm.com