Poisson's ratio measures the ratio of lateral strain to axial strain when a material is stretched or compressed, revealing how materials deform under mechanical stress. Understanding this key property helps predict material behavior in engineering, construction, and product design. Discover more about Poisson's ratio and its critical role in material science in the following sections.
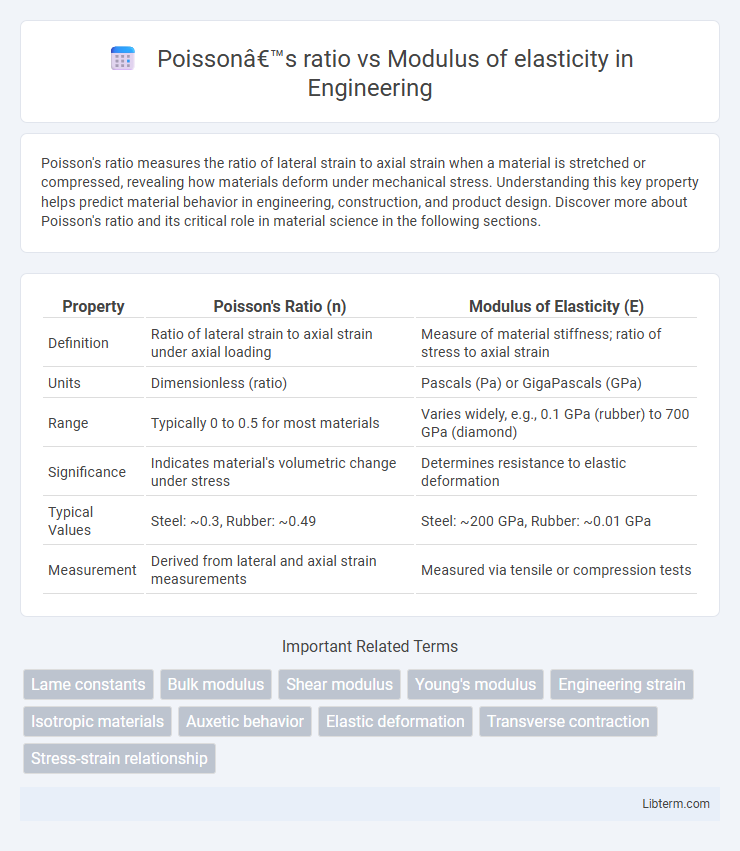
Table of Comparison
| Property | Poisson's Ratio (n) | Modulus of Elasticity (E) |
|---|---|---|
| Definition | Ratio of lateral strain to axial strain under axial loading | Measure of material stiffness; ratio of stress to axial strain |
| Units | Dimensionless (ratio) | Pascals (Pa) or GigaPascals (GPa) |
| Range | Typically 0 to 0.5 for most materials | Varies widely, e.g., 0.1 GPa (rubber) to 700 GPa (diamond) |
| Significance | Indicates material's volumetric change under stress | Determines resistance to elastic deformation |
| Typical Values | Steel: ~0.3, Rubber: ~0.49 | Steel: ~200 GPa, Rubber: ~0.01 GPa |
| Measurement | Derived from lateral and axial strain measurements | Measured via tensile or compression tests |
Introduction to Poisson’s Ratio and Modulus of Elasticity
Poisson's ratio measures the negative ratio of transverse to axial strain in a material subjected to uniaxial stress, typically ranging between 0 and 0.5 for most engineering materials, indicating how much a material deforms laterally when stretched or compressed. Modulus of elasticity, or Young's modulus, quantifies a material's stiffness by defining the ratio of longitudinal stress to longitudinal strain within the elastic limit. Together, these fundamental mechanical properties characterize elastic behavior, informing material selection and structural analysis in engineering applications.
Defining Poisson’s Ratio: Meaning and Significance
Poisson's ratio measures the ratio of transverse strain to axial strain in materials under stress, reflecting how materials deform laterally when stretched or compressed. It is a dimensionless quantity typically ranging between 0 and 0.5 for most engineering materials, indicating the ductility and volumetric changes during deformation. Unlike the modulus of elasticity, which quantifies a material's stiffness or resistance to elastic deformation, Poisson's ratio provides critical insights into the material's deformation behavior and structural integrity under load.
Understanding Modulus of Elasticity: Concept and Calculation
Modulus of elasticity, also known as Young's modulus, measures a material's stiffness by quantifying the ratio of stress to strain within the elastic deformation range. It is calculated using the formula E = s/e, where E is the modulus of elasticity, s represents the applied stress, and e denotes the resulting strain. While Poisson's ratio describes the lateral strain to axial strain relationship during deformation, the modulus of elasticity specifically reflects the material's resistance to axial stretching or compression.
Fundamental Differences: Poisson’s Ratio vs Modulus of Elasticity
Poisson's ratio is a dimensionless measure of the lateral strain to axial strain in a material under tensile or compressive stress, reflecting the material's tendency to expand or contract perpendicular to the applied force. Modulus of elasticity, also known as Young's modulus, quantifies a material's stiffness by defining the ratio of axial stress to axial strain within the elastic deformation range. While Poisson's ratio characterizes deformation geometry, the modulus of elasticity assesses material rigidity, making both essential yet fundamentally different parameters in material science and engineering analysis.
Mathematical Relationships between Poisson’s Ratio and Modulus of Elasticity
Poisson's ratio (n) and modulus of elasticity (E) are interconnected through material constants such as shear modulus (G) and bulk modulus (K), with E expressed as E = 2G(1 + n) and also E = 3K(1 - 2n). These equations highlight the dependency of the elastic modulus on Poisson's ratio, where higher values of n indicate greater lateral strain relative to axial strain under loading. Precise calculation of mechanical properties in isotropic materials often relies on these mathematical relationships to characterize elasticity and deformation behavior.
Material Behavior: Impact of Poisson’s Ratio and Modulus of Elasticity
Poisson's ratio quantifies the lateral strain response of a material under axial loading, influencing volumetric changes and deformation patterns during stress application. The modulus of elasticity measures a material's stiffness, determining its ability to resist elastic deformation when subjected to stress. Together, Poisson's ratio and the modulus of elasticity provide critical insights into material behavior, affecting stress distribution, structural stability, and failure mechanisms in engineering applications.
Applications in Engineering: Why Both Properties Matter
Poisson's ratio and modulus of elasticity are critical for predicting material behavior under load, where the modulus quantifies stiffness and Poisson's ratio indicates lateral strain response. In engineering design, these properties influence stress analysis, structural stability, and deformation predictions for components like beams, columns, and pressure vessels. Accurate values for both enable optimized material selection and enhance safety and performance in civil, mechanical, and aerospace engineering applications.
Measurement Techniques: Determining Poisson’s Ratio and Modulus of Elasticity
Poisson's ratio is measured by simultaneously capturing lateral and axial strain using strain gauges or Digital Image Correlation (DIC) during tensile or compressive testing, providing a ratio of transverse contraction to longitudinal extension. Modulus of elasticity, often determined via tensile tests, is calculated from the slope of the linear elastic region on the stress-strain curve, using extensometers or strain gauges for precise axial strain measurement. Advanced methods like ultrasonic pulse velocity and nanoindentation also offer non-destructive evaluation of elastic modulus while maintaining accuracy in diverse material testing scenarios.
Real-World Examples and Case Studies
Poisson's ratio and modulus of elasticity are critical parameters in material science, influencing structural behavior in real-world applications such as aerospace, civil engineering, and biomechanics. High modulus materials like steel exhibit low deformation under stress but a distinct Poisson's ratio that affects lateral strain, crucial in bridge design to prevent failure. Case studies of composite materials in wind turbine blades reveal how altering Poisson's ratio improves energy efficiency by balancing stiffness and flexibility.
Conclusion: Choosing the Right Parameter for Material Selection
Poisson's ratio and modulus of elasticity serve distinct roles in material selection, with Poisson's ratio characterizing the lateral strain response under axial loading and modulus of elasticity quantifying material stiffness. For applications demanding precise deformation prediction and load-bearing capacity, modulus of elasticity provides a critical measure of rigidity and structural behavior. Poisson's ratio becomes essential when understanding volumetric changes and multi-axial strain states, making simultaneous consideration necessary for comprehensive material analysis and optimal engineering design.
Poisson’s ratio Infographic
 libterm.com
libterm.com