Nominal stress is the average stress calculated by dividing the applied force by the original cross-sectional area of a material, without considering any changes in dimensions due to deformation. It is a fundamental concept in mechanical engineering for analyzing material strength and predicting failure under load. Explore the article to understand how nominal stress relates to real-world applications and material behavior.
Table of Comparison
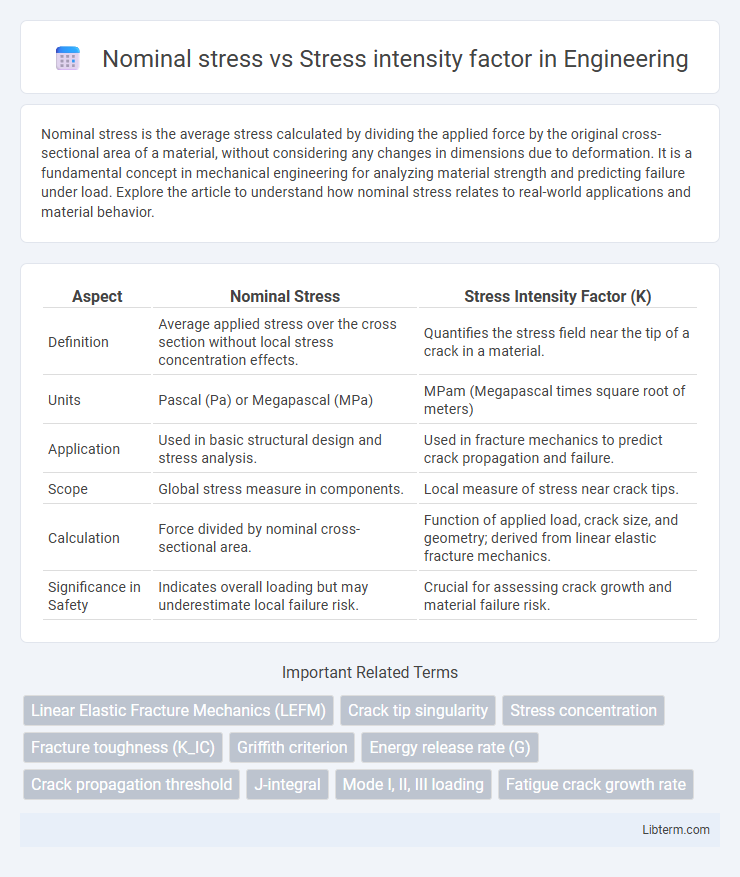
| Aspect | Nominal Stress | Stress Intensity Factor (K) |
|---|---|---|
| Definition | Average applied stress over the cross section without local stress concentration effects. | Quantifies the stress field near the tip of a crack in a material. |
| Units | Pascal (Pa) or Megapascal (MPa) | MPam (Megapascal times square root of meters) |
| Application | Used in basic structural design and stress analysis. | Used in fracture mechanics to predict crack propagation and failure. |
| Scope | Global stress measure in components. | Local measure of stress near crack tips. |
| Calculation | Force divided by nominal cross-sectional area. | Function of applied load, crack size, and geometry; derived from linear elastic fracture mechanics. |
| Significance in Safety | Indicates overall loading but may underestimate local failure risk. | Crucial for assessing crack growth and material failure risk. |
Introduction to Nominal Stress and Stress Intensity Factor
Nominal stress represents the average stress over a cross-sectional area without considering the presence of flaws or cracks, serving as a basic measure in structural analysis. Stress intensity factor (K) quantifies the stress state near the tip of a crack, incorporating the effect of crack size and loading conditions, critical for fracture mechanics assessments. Understanding both nominal stress and stress intensity factor enables accurate prediction of material failure and structural integrity under various loading scenarios.
Definitions: Nominal Stress vs Stress Intensity Factor
Nominal stress refers to the average stress calculated by dividing the applied load by the cross-sectional area of a material, providing a simplified measure of stress without accounting for stress concentrations or flaws. Stress intensity factor (K) quantifies the stress state near the tip of a crack, incorporating the effect of crack size, loading, and geometry to predict the onset of fracture. While nominal stress is used for general stress analysis, the stress intensity factor is essential in fracture mechanics for assessing crack propagation and failure risk.
Fundamental Differences between Nominal Stress and Stress Intensity Factor
Nominal stress refers to the average stress calculated by dividing the applied load by the cross-sectional area, providing a simplified measure used in basic structural analysis. Stress intensity factor (SIF), denoted as K, quantifies the stress state near the tip of a crack and is critical in fracture mechanics for predicting crack growth and failure. The fundamental difference lies in nominal stress being a global measure applied to uniform sections, while the stress intensity factor is a local parameter that characterizes stress concentration effects at crack tips under different loading modes.
Calculation Methods for Nominal Stress
Nominal stress is calculated by dividing the applied load by the original cross-sectional area of the material, providing a straightforward measure of stress before accounting for stress concentrations. This calculation method assumes uniform stress distribution, which simplifies analysis but may underestimate localized stresses near flaws or geometric discontinuities. In contrast, the stress intensity factor incorporates fracture mechanics principles to quantify the stress state near crack tips, making nominal stress calculations essential for initial design but insufficient for assessing fracture risk in cracked components.
Calculation Methods for Stress Intensity Factor
The calculation methods for Stress Intensity Factor (SIF) primarily involve analytical solutions, numerical techniques like Finite Element Analysis (FEA), and empirical formulas derived from experimental data. Analytical methods apply fracture mechanics principles to idealized crack geometries, while FEA provides detailed stress distribution around crack tips for complex geometries and loading conditions. Empirical formulas relate nominal stress, crack size, and geometry factors to estimate the SIF, enabling engineers to predict crack propagation and failure in structural components.
Applications in Engineering Design and Failure Analysis
Nominal stress provides a simplified measure of average stress used in preliminary engineering design to estimate load-bearing capacity of components, while the stress intensity factor quantifies the severity of stress concentration near crack tips, crucial for fracture mechanics analysis. In failure analysis, the stress intensity factor enables prediction of crack growth and critical fracture conditions, enhancing safety assessments beyond nominal stress estimates. Engineering design integrates nominal stress for routine loading scenarios and employs stress intensity factors specifically for assessing structural integrity in cracked or damaged materials.
Role in Fracture Mechanics and Material Testing
Nominal stress represents the average applied load over the cross-sectional area of a material, serving as a basic measure in fracture mechanics for initial assessment of material strength. Stress intensity factor (K) quantifies the stress state near the tip of a crack, providing critical insight into crack propagation and fracture toughness under varying loading conditions. The stress intensity factor is fundamental in predicting failure in material testing and structural integrity evaluations, surpassing nominal stress in accuracy for crack growth analysis.
Advantages and Limitations of Each Approach
Nominal stress provides a simplified measure of average stress over a cross-sectional area, making it easy to calculate for preliminary design assessments but lacks accuracy near crack tips where stress concentration occurs. Stress intensity factor (SIF) offers a precise quantification of the stress state at crack tips, essential for fracture mechanics analysis and predicting crack propagation, though it requires complex calculations and detailed knowledge of crack geometry and loading conditions. Nominal stress is advantageous for straightforward scenarios and quick evaluations, while SIF is indispensable for reliable failure predictions in components experiencing fatigue or fracture.
Case Studies: Comparative Analysis of Nominal Stress and Stress Intensity Factor
Case studies comparing nominal stress and stress intensity factor demonstrate that stress intensity factors provide a more accurate assessment of crack tip stress fields, especially in fracture mechanics applications. Nominal stress often underestimates the severity of stress concentrations near flaws, leading to less reliable predictions of material failure. Empirical data reveal that stress intensity factor-based analyses significantly improve failure predictions in cracked components across aerospace, automotive, and structural engineering.
Conclusion: Choosing the Appropriate Stress Measure
Nominal stress provides a simplified average stress value useful for general design calculations but often underestimates local stress concentrations near flaws or cracks. The stress intensity factor (K) offers a more precise measure of stress behavior at crack tips, essential for fracture mechanics and predicting crack propagation under loading. Selecting between nominal stress and stress intensity factor depends on the failure mode analysis, with K being critical for materials prone to brittle fracture and nominal stress adequate for ductile materials with uniform stress distribution.
Nominal stress Infographic
 libterm.com
libterm.com