Long exact sequences reveal intricate relationships between algebraic structures, often arising from short exact sequences or homology theories. These sequences enable you to understand how objects like groups or modules transform under various operations, making them essential tools in algebraic topology and homological algebra. Discover more about their construction and applications in the rest of the article.
Table of Comparison
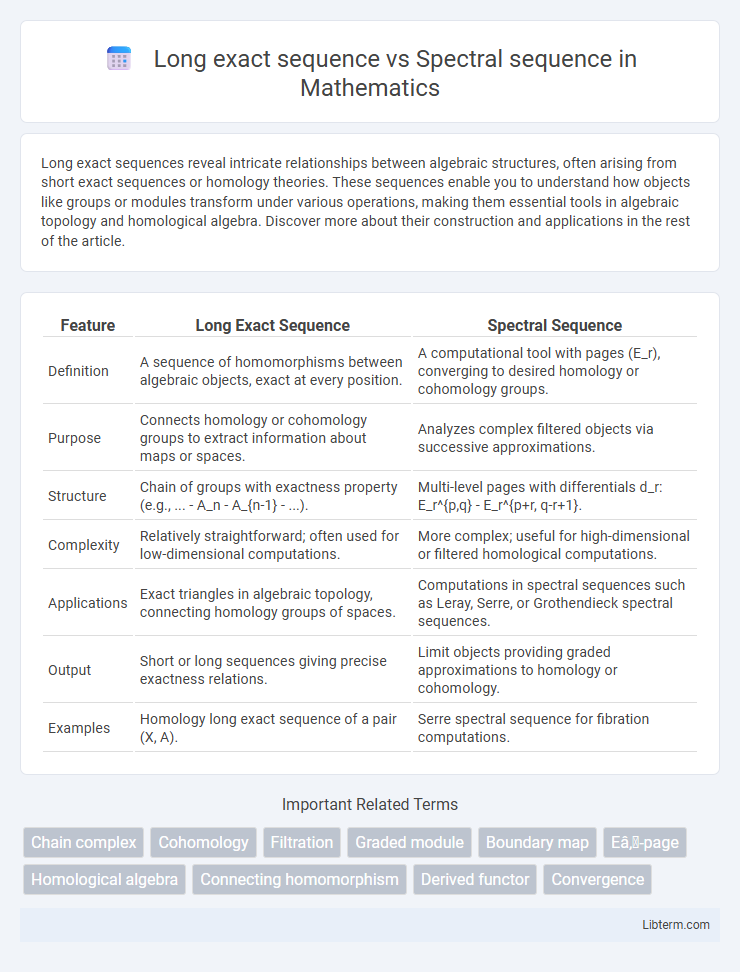
| Feature | Long Exact Sequence | Spectral Sequence |
|---|---|---|
| Definition | A sequence of homomorphisms between algebraic objects, exact at every position. | A computational tool with pages (E_r), converging to desired homology or cohomology groups. |
| Purpose | Connects homology or cohomology groups to extract information about maps or spaces. | Analyzes complex filtered objects via successive approximations. |
| Structure | Chain of groups with exactness property (e.g., ... - A_n - A_{n-1} - ...). | Multi-level pages with differentials d_r: E_r^{p,q} - E_r^{p+r, q-r+1}. |
| Complexity | Relatively straightforward; often used for low-dimensional computations. | More complex; useful for high-dimensional or filtered homological computations. |
| Applications | Exact triangles in algebraic topology, connecting homology groups of spaces. | Computations in spectral sequences such as Leray, Serre, or Grothendieck spectral sequences. |
| Output | Short or long sequences giving precise exactness relations. | Limit objects providing graded approximations to homology or cohomology. |
| Examples | Homology long exact sequence of a pair (X, A). | Serre spectral sequence for fibration computations. |
Introduction to Homological Tools
Long exact sequences provide a straightforward method to relate homology groups of chain complexes through connecting homomorphisms, essential for tracking algebraic invariants in topological spaces. Spectral sequences offer a more powerful computational framework, breaking complex homological problems into manageable layers and converging toward desired homological or cohomological invariants. Both tools serve as foundational techniques in homological algebra and algebraic topology, enabling deeper analysis of filtered complexes and exact couples.
Defining Long Exact Sequences
Long exact sequences are pivotal algebraic tools that connect homology or cohomology groups across multiple dimensions through a chain of morphisms, preserving exactness at each stage. They arise naturally in contexts such as the homology of pairs in algebraic topology, reflecting precise algebraic relationships among groups and facilitating computations of unknown terms from known ones. Unlike spectral sequences that provide a filtered, iterative approach to approximating homological invariants, long exact sequences deliver direct, stepwise connections crucial for understanding exactness properties in chain complexes.
What is a Spectral Sequence?
A spectral sequence is an algebraic tool used to compute homology or cohomology groups by filtering complex structures into successive approximations, organized in pages or terms with differentials connecting them. It generalizes the concept of a long exact sequence by providing a multi-layered framework that converges to the desired invariant, often employed in algebraic topology, homological algebra, and algebraic geometry. Spectral sequences enable systematic computation where direct application of long exact sequences is infeasible due to complexity or layered filtrations.
Key Differences in Structure
Long exact sequences consist of a chain of groups or modules connected by homomorphisms, where the image of one map equals the kernel of the next, allowing for precise computations of homology or cohomology in a linear, sequential format. Spectral sequences present a two-dimensional array of groups equipped with differentials that converge to graded pieces of a target homology or cohomology, effectively organizing complex filtrations and successive approximations across multiple pages. The fundamental structural difference lies in the linear progression of long exact sequences versus the multi-layered, iterated approximations and convergence process inherent in spectral sequences.
Typical Applications in Algebra and Topology
Long exact sequences are crucial in algebra and topology for analyzing homology and cohomology groups, particularly in connecting the algebraic invariants of related spaces or chain complexes, such as in the Mayer-Vietoris sequence or exact sequences of homotopy groups. Spectral sequences provide a powerful computational tool to systematically approximate complex homological structures, making them essential in filtrations, fiber bundles, and derived functor analysis where multi-stage convergence yields detailed information about graded objects. Both techniques complement each other in resolving extension problems and deep structural properties of algebraic topology, homological algebra, and sheaf cohomology.
Advantages and Limitations of Long Exact Sequences
Long exact sequences provide a straightforward and intuitive tool for tracking homological or cohomological information across algebraic or topological structures, making them essential in classical algebraic topology and homological algebra. Their main advantage lies in the clarity and directness they offer for understanding relationships between consecutive homology or cohomology groups, but they can become cumbersome or insufficient when dealing with complex filtrations or multi-graded structures. The limitation of long exact sequences is their inability to efficiently handle filtrations or hierarchies of substructures, where spectral sequences excel by systematically approximating and converging to the desired homological invariants.
Power and Complexity of Spectral Sequences
Spectral sequences provide a powerful computational framework that generalizes long exact sequences by systematically approximating homology or cohomology groups through successive pages of differentials, enabling the resolution of complex algebraic and topological problems. Unlike long exact sequences, which offer direct relations between adjacent homology groups, spectral sequences manage intricate filtrations and multi-layered structures, capturing higher-order extensions and interactions that are intractable with simpler tools. The increased complexity and computational depth of spectral sequences allow for effective analysis of filtered complexes, fibers in fibrations, and graded objects, making them indispensable in modern algebraic topology and homological algebra.
Transition: When to Use Which Sequence
Long exact sequences are ideal for straightforward homological algebra problems involving short exact sequences, providing clear step-by-step connections between homology groups. Spectral sequences offer a powerful framework for complex filtrations or multi-layered structures, converging through successive approximations to compute homology or cohomology groups that are otherwise intractable. Use long exact sequences for direct computations in simpler cases, while spectral sequences should be chosen when dealing with filtered complexes, fibrations, or spectral filtrations requiring iterative refinement.
Examples Illustrating Both Techniques
Long exact sequences arise naturally in homology and cohomology theories, such as the Mayer-Vietoris sequence for decomposing topological spaces or the long exact sequence of a pair (X, A) in singular homology. Spectral sequences provide a powerful computational tool in complex filtered complexes or double complexes, exemplified by the Leray-Serre spectral sequence used to compute the homology of a fiber bundle from the homology of its base and fiber. While long exact sequences give direct algebraic relations between adjacent homological degrees, spectral sequences encode multistage approximations converging to desired homological invariants, illustrated concretely by the calculation of Ext and Tor groups in homological algebra.
Conclusion: Choosing the Appropriate Tool
Long exact sequences provide a straightforward method for computing homology or cohomology groups when dealing with short exact sequences or filtrations with few steps. Spectral sequences offer a powerful computational framework for handling complex filtered complexes and multi-step filtrations by converging to the desired homology groups through successive approximations. Choosing between these tools depends on the problem's complexity: long exact sequences excel in simpler contexts, while spectral sequences are essential for intricate structures requiring stepwise analysis.
Long exact sequence Infographic
 libterm.com
libterm.com