Regression analyzes the relationship between variables to predict outcomes based on historical data, essential for making informed decisions in various fields such as finance, marketing, and healthcare. Understanding different types of regression models, including linear, logistic, and polynomial, can enhance your ability to interpret data accurately and improve forecasting precision. Explore the rest of this article to uncover how regression techniques can transform your data insights.
Table of Comparison
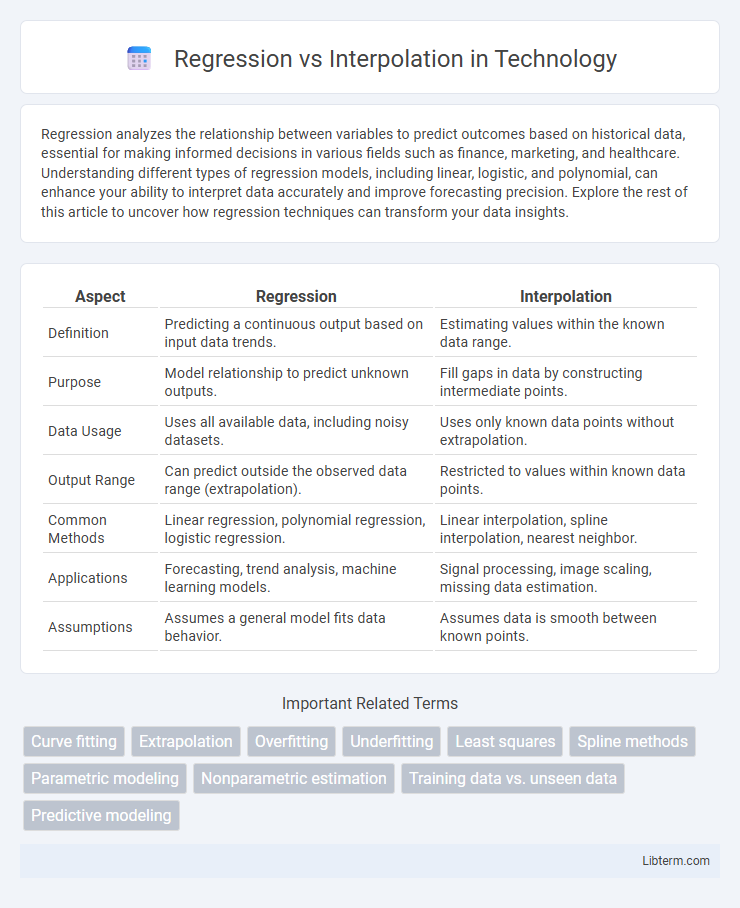
| Aspect | Regression | Interpolation |
|---|---|---|
| Definition | Predicting a continuous output based on input data trends. | Estimating values within the known data range. |
| Purpose | Model relationship to predict unknown outputs. | Fill gaps in data by constructing intermediate points. |
| Data Usage | Uses all available data, including noisy datasets. | Uses only known data points without extrapolation. |
| Output Range | Can predict outside the observed data range (extrapolation). | Restricted to values within known data points. |
| Common Methods | Linear regression, polynomial regression, logistic regression. | Linear interpolation, spline interpolation, nearest neighbor. |
| Applications | Forecasting, trend analysis, machine learning models. | Signal processing, image scaling, missing data estimation. |
| Assumptions | Assumes a general model fits data behavior. | Assumes data is smooth between known points. |
Introduction to Regression and Interpolation
Regression analyzes the relationship between dependent and independent variables to predict continuous outcomes, using methods like linear or polynomial regression. Interpolation estimates unknown data points within the range of a discrete set of known data points, commonly employing techniques such as linear, spline, or nearest-neighbor interpolation. Both methods are essential in data analysis, with regression focusing on modeling trends and interpolation emphasizing precise value estimation within datasets.
Defining Regression: Purpose and Applications
Regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables, aiming to predict continuous outcomes and identify trends. It is widely applied in fields such as economics, biology, and machine learning for tasks like forecasting sales, analyzing experimental data, and optimizing algorithms. Regression techniques include linear regression, polynomial regression, and logistic regression, each suited for different types of data and analysis goals.
Understanding Interpolation: Key Concepts
Interpolation estimates unknown values within the range of a discrete set of known data points, ensuring a smooth curve that passes exactly through those points. Key techniques include linear interpolation, polynomial interpolation, and spline interpolation, each varying in complexity and fitting accuracy. Understanding interpolation is crucial for applications requiring precise intermediate value predictions, such as computer graphics, signal processing, and numerical analysis.
Similarities Between Regression and Interpolation
Both regression and interpolation aim to model the relationship between variables by fitting a function to data points, enabling prediction within a given range. They utilize underlying mathematical models, such as polynomial or linear equations, to estimate unknown values based on known observations. Both techniques serve as essential tools in data analysis and machine learning to infer trends and patterns from datasets.
Fundamental Differences: Regression vs Interpolation
Regression estimates the underlying functional relationship between variables by fitting a model that minimizes prediction error, often generalizing beyond the observed data points. Interpolation precisely predicts unknown values within the range of the observed dataset by constructing a function that passes exactly through all given data points. The fundamental difference lies in regression's approximation approach aimed at capturing trends, while interpolation emphasizes exact value recovery within the sample range.
Types of Regression Techniques
Linear regression models the relationship between dependent and independent variables by fitting a straight line, making it ideal for continuous data prediction. Polynomial regression extends linear regression by fitting a curve, capturing nonlinear patterns through higher-degree polynomial terms. Other types like Ridge and Lasso regression incorporate regularization to prevent overfitting, while Logistic regression focuses on classification tasks by modeling probabilities.
Common Interpolation Methods
Common interpolation methods include linear interpolation, which estimates unknown values by connecting two adjacent data points with a straight line, and polynomial interpolation, using high-degree polynomials to fit a curve through all data points. Spline interpolation offers a piecewise polynomial approach, typically cubic splines, ensuring smoothness at the data points and better handling of large datasets. Unlike regression, interpolation methods aim to precisely fit the given data points without minimizing overall error or predicting trends outside the data range.
When to Use Regression Over Interpolation
Use regression over interpolation when modeling relationships with noisy or incomplete data to estimate trends beyond observed points. Regression accommodates uncertainty by fitting a best-fit curve and predicts outcomes outside the sample range, whereas interpolation strictly estimates within known data intervals. Choose regression for predictive analytics, trend analysis, or when capturing underlying patterns in real-world datasets.
Advantages and Limitations of Each Approach
Regression provides a powerful tool for modeling relationships in data and predicting outcomes beyond observed values, offering flexibility through various model types like linear, polynomial, and logistic regression. However, it may suffer from overfitting or underfitting depending on model complexity and requires assumptions such as linearity or normality that may not always hold. Interpolation accurately estimates values within the range of known data points, ensuring exact fit and smooth transitions but fails to predict beyond the observed data range and can become unreliable with noisy or unevenly spaced data.
Practical Examples and Use Cases
Regression models predict continuous outcomes by fitting a line or curve to observed data points, as seen in housing price estimation based on factors like size and location. Interpolation estimates values within the range of known data points, such as calculating intermediate weather temperatures from sensor readings at discrete times. Practical use cases of regression include sales forecasting and risk assessment, while interpolation is widely used in digital image processing and geographic information systems (GIS) for filling data gaps.
Regression Infographic
 libterm.com
libterm.com