Understanding the optimal duration for various activities can significantly improve your productivity and well-being. Whether it's exercise, work sessions, or relaxation, knowing how much time to allocate helps balance efficiency with rest. Explore the full article to discover how to tailor your schedule for maximum benefit.
Table of Comparison
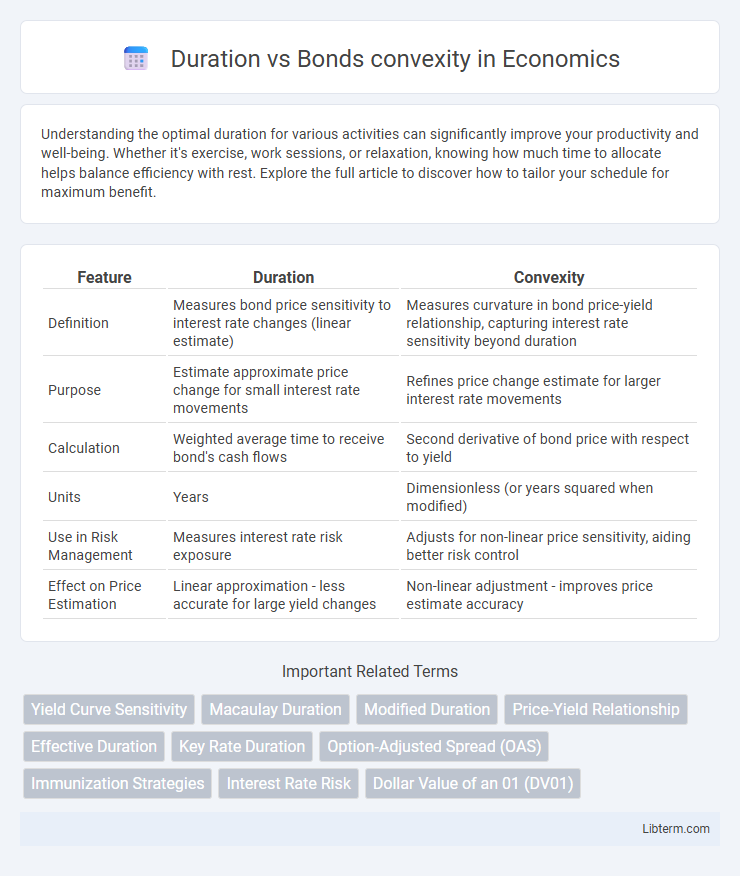
| Feature | Duration | Convexity |
|---|---|---|
| Definition | Measures bond price sensitivity to interest rate changes (linear estimate) | Measures curvature in bond price-yield relationship, capturing interest rate sensitivity beyond duration |
| Purpose | Estimate approximate price change for small interest rate movements | Refines price change estimate for larger interest rate movements |
| Calculation | Weighted average time to receive bond's cash flows | Second derivative of bond price with respect to yield |
| Units | Years | Dimensionless (or years squared when modified) |
| Use in Risk Management | Measures interest rate risk exposure | Adjusts for non-linear price sensitivity, aiding better risk control |
| Effect on Price Estimation | Linear approximation - less accurate for large yield changes | Non-linear adjustment - improves price estimate accuracy |
Understanding Duration: A Key Bond Metric
Duration measures a bond's sensitivity to interest rate changes, indicating the approximate percentage price change for a 1% shift in yields. It quantifies the weighted average time to receive all cash flows and serves as a first-order estimate of interest rate risk. Bonds with higher duration experience greater price volatility, making it essential for investors to assess duration alongside convexity for more accurate risk management.
What is Bond Convexity?
Bond convexity measures the curvature in the relationship between bond prices and interest rates, reflecting how much a bond's duration changes as yields fluctuate. It provides a more accurate estimate of bond price sensitivity by accounting for interest rate volatility beyond the linear approximation given by duration. Higher convexity indicates greater price sensitivity to interest rate changes, offering investors better risk assessment and portfolio management tools.
Duration vs Convexity: Core Differences
Duration measures a bond's price sensitivity to changes in interest rates, approximating price changes linearly for small rate movements. Convexity captures the curvature of the price-yield relationship, accounting for the acceleration of price changes when yields shift substantially. Core differences lie in duration's linear estimate versus convexity's adjustment for nonlinear price behavior, making convexity a more accurate tool for managing interest rate risk in large yield fluctuations.
How Duration Measures Interest Rate Risk
Duration quantifies a bond's sensitivity to interest rate changes by estimating the percentage price change for a 1% shift in yields, serving as a linear approximation of interest rate risk. Convexity complements duration by capturing the curvature of the price-yield relationship, providing a more accurate measure for larger interest rate movements. Understanding duration helps investors gauge potential price volatility, while convexity adjusts for nonlinear price behavior, enhancing risk management in bond portfolios.
The Role of Convexity in Bond Price Sensitivity
Convexity measures the curvature in the relationship between bond prices and yields, capturing the degree to which duration changes as interest rates fluctuate. While duration estimates a bond's linear price sensitivity to interest rate changes, convexity accounts for the nonlinear effects, providing a more accurate approximation, especially for large yield shifts. Higher convexity in bonds results in greater price increases when yields decline and smaller price decreases when yields rise, enhancing the bond's risk-return profile.
Types of Duration: Macaulay, Modified, and Effective
Macaulay duration measures the weighted average time until a bond's cash flows are received, serving as the foundation for assessing interest rate risk. Modified duration adjusts Macaulay duration to estimate a bond's price sensitivity to changes in yield, reflecting linear price changes under small interest rate movements. Effective duration incorporates potential changes in cash flows due to embedded options, providing a more accurate measure of convexity and interest rate risk for callable or puttable bonds.
Positive vs Negative Convexity Explained
Positive convexity in bonds means that as interest rates fall, bond prices increase at an accelerating rate, enhancing price gains and reducing interest rate risk. Negative convexity occurs when bond prices increase at a decreasing rate or decline faster as rates drop, common in callable bonds due to the call option limiting price appreciation. Understanding the difference between duration, which measures price sensitivity linearly, and convexity, which captures the curvature of price changes, is essential for managing bond portfolio risks effectively.
The Significance of Duration and Convexity in Portfolio Management
Duration measures a bond's sensitivity to interest rate changes, providing a linear estimate of price volatility, while convexity accounts for the curvature, enhancing accuracy in price predictions for larger rate shifts. Incorporating both duration and convexity in portfolio management improves risk assessment by capturing interest rate risk more comprehensively, leading to better-informed hedging and allocation decisions. This dual consideration helps optimize bond portfolio performance by balancing yield and risk, especially in volatile or shifting interest rate environments.
Limitations of Relying Solely on Duration
Duration measures a bond's sensitivity to interest rate changes but assumes a linear price-yield relationship, which limits accuracy for large yield shifts. Convexity accounts for the curvature in the price-yield curve, providing a more precise estimation of price changes under significant interest rate movements. Relying solely on duration ignores convexity effects, potentially leading to underestimation of risk and mispricing in volatile markets.
Combining Duration and Convexity for Optimal Bond Analysis
Combining duration and convexity enhances bond analysis by capturing both linear and nonlinear price sensitivities to interest rate changes. Duration measures the approximate percentage price change for small yield shifts, while convexity adjusts for the curvature of price-yield relationship, improving accuracy for larger fluctuations. Integrating these metrics allows investors to better estimate bond price volatility, manage interest rate risk, and optimize portfolio immunization strategies.
Duration Infographic
 libterm.com
libterm.com