The CES (Constant Elasticity of Substitution) production function models the relationship between inputs and output by allowing a flexible substitution rate between factors of production while maintaining constant elasticity. It generalizes the Cobb-Douglas and Leontief production functions, providing a more versatile tool for analyzing how different input combinations affect productivity. Explore the rest of the article to understand how CES functions can optimize Your production decisions.
Table of Comparison
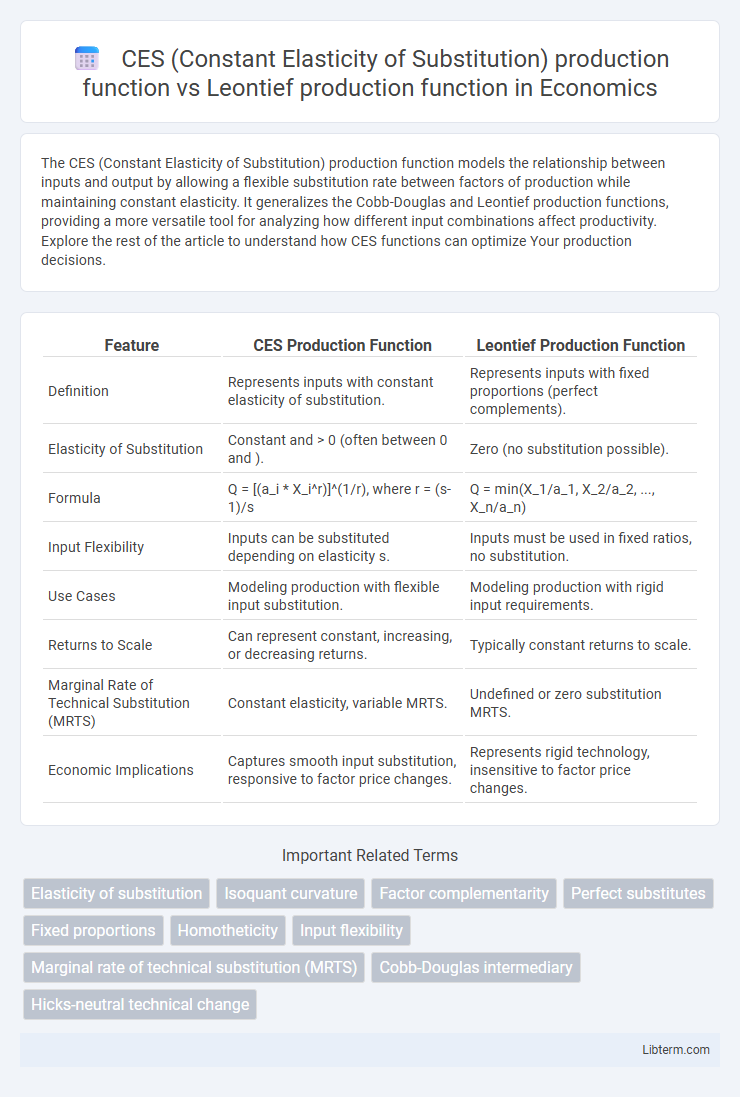
| Feature | CES Production Function | Leontief Production Function |
|---|---|---|
| Definition | Represents inputs with constant elasticity of substitution. | Represents inputs with fixed proportions (perfect complements). |
| Elasticity of Substitution | Constant and > 0 (often between 0 and ). | Zero (no substitution possible). |
| Formula | Q = [(a_i * X_i^r)]^(1/r), where r = (s-1)/s | Q = min(X_1/a_1, X_2/a_2, ..., X_n/a_n) |
| Input Flexibility | Inputs can be substituted depending on elasticity s. | Inputs must be used in fixed ratios, no substitution. |
| Use Cases | Modeling production with flexible input substitution. | Modeling production with rigid input requirements. |
| Returns to Scale | Can represent constant, increasing, or decreasing returns. | Typically constant returns to scale. |
| Marginal Rate of Technical Substitution (MRTS) | Constant elasticity, variable MRTS. | Undefined or zero substitution MRTS. |
| Economic Implications | Captures smooth input substitution, responsive to factor price changes. | Represents rigid technology, insensitive to factor price changes. |
Introduction to Production Functions
The CES (Constant Elasticity of Substitution) production function allows for varying degrees of substitutability between inputs, characterized by a constant elasticity parameter that measures the ease of input substitution. The Leontief production function represents a fixed-proportion technology with zero substitutability, where inputs must be used in rigid, predetermined ratios. These production functions capture different economic realities by modeling how input combinations impact output, influencing resource allocation and efficiency analysis in production theory.
Overview of CES Production Function
The CES (Constant Elasticity of Substitution) production function generalizes the Cobb-Douglas and Leontief functions by allowing a constant substitution elasticity between inputs, capturing a broader range of input substitutability. Unlike the Leontief production function, which assumes fixed input proportions with zero substitutability, the CES function introduces a parameter that governs the flexibility in input substitution, enabling analysis of varying degrees of input replaceability. This property makes the CES function particularly valuable for modeling production processes where input flexibility influences output efficiency across different economic conditions.
Overview of Leontief Production Function
The Leontief production function models output as a fixed-proportion combination of inputs, assuming zero substitutability between them, which contrasts with the CES production function's flexible substitution elasticity. This function is represented by the minimum of input quantities scaled by technical coefficients, reflecting rigid input requirements in production processes. It is extensively used in input-output analysis and industries where inputs must be used in strict ratios, emphasizing technological constraints over input flexibility.
Mathematical Formulation of CES and Leontief Functions
The CES (Constant Elasticity of Substitution) production function is mathematically expressed as \( Q = A \left( \delta K^{-\rho} + (1-\delta) L^{-\rho} \right)^{-\frac{1}{\rho}} \), where \( Q \) is output, \( K \) is capital, \( L \) is labor, \( A \) is total factor productivity, \( \delta \) represents distribution parameter, and \( \rho = \frac{1}{\sigma} - 1 \) with \( \sigma \) being the elasticity of substitution between inputs. The Leontief production function takes the form \( Q = \min \left( \frac{K}{a}, \frac{L}{b} \right) \), emphasizing fixed input proportions where \( a \) and \( b \) are the input coefficients for capital and labor respectively. While CES allows for varying degrees of substitutability between inputs, the Leontief function assumes zero substitutability, reflecting perfect complementarity in production.
Key Assumptions and Properties
The CES production function assumes a constant elasticity of substitution between inputs, allowing a smooth substitutability characterized by the parameter s, where s > 0 and controls the ease of input substitution, contrasted with the Leontief production function which assumes no substitutability, representing inputs as perfect complements with a fixed proportions requirement (s = 0). CES functions exhibit properties of homogeneity of degree one and continuous differentiability, enabling marginal rates of technical substitution to vary smoothly, while Leontief functions are non-differentiable at points except along rays where input proportions are held constant, reflecting rigid input combination constraints. Key assumptions for CES include flexibility in input choice and scalable production, whereas Leontief assumes rigid fixed input ratios with zero elasticity of substitution, often modeling processes where inputs must be combined in exact fixed proportions without substitution possibilities.
Substitutability of Inputs: CES vs Leontief
The CES (Constant Elasticity of Substitution) production function allows for varying degrees of input substitutability, characterized by its elasticity parameter that can range from perfect substitutes to perfect complements. In contrast, the Leontief production function assumes zero substitutability between inputs, modeling them as fixed-proportion complements where inputs must be used in strict ratios. This fundamental difference makes CES more flexible for representing production processes with intermediate substitutability, while Leontief is suited for systems where inputs are rigidly combined.
Graphical Representation and Isoquants Analysis
CES production functions feature smooth, convex isoquants reflecting varying degrees of substitutability between inputs, with elasticity of substitution parameter controlling the curvature. Leontief production functions have L-shaped isoquants representing perfect complementarity, indicating zero substitutability and fixed input proportions. Graphically, CES isoquants allow for input trade-offs along curves, while Leontief isoquants restrict input combinations to rigid corners where inputs must be used in fixed ratios.
Real-World Applications and Examples
The CES production function is widely used in economic modeling where substitution between inputs like labor and capital is flexible, such as in aggregate national production or energy economics, capturing technological changes and varying factor shares. The Leontief production function is applied in input-output analysis and sectors with fixed input proportions, like agriculture or manufacturing processes involving rigid machinery-to-labor ratios, highlighting non-substitutable resource dependencies. Industry applications of CES include evaluating policy impacts on technological adaptation, while Leontief models aid in supply chain optimization and environmental impact assessments where inputs are complementary.
Advantages and Limitations of Each Function
The CES production function offers flexibility in substituting inputs with a constant elasticity parameter, enabling firms to model varying degrees of input substitutability and adapt to changing technological conditions, but it may involve complex estimation and requires precise parameter calibration. The Leontief production function assumes fixed input proportions and no substitutability, providing simplicity and clear input-output relationships, yet it lacks flexibility to represent technological substitution and may oversimplify production processes. CES functions are advantageous for analyzing substitution effects and technological change, while Leontief functions excel in modeling rigid production systems but are limited in capturing input flexibility.
Choosing Between CES and Leontief: Practical Considerations
Choosing between CES and Leontief production functions hinges on the substitutability of inputs; CES allows for variable elasticity, capturing a continuum from perfect substitutes to fixed proportions, while Leontief assumes zero substitutability with fixed input ratios. Practical application favors CES in industries where flexibility and technological changes affect input combinations, whereas Leontief suits processes with rigid input requirements, such as assembly lines or natural resource extraction. Empirical data on input substitutability and technological constraints guide the selection to ensure accurate modeling of production processes.
CES (Constant Elasticity of Substitution) production function Infographic
 libterm.com
libterm.com