The Tobit model is a statistical approach designed to estimate linear relationships between variables when there is either left- or right-censoring in the dependent variable, often occurring in limited dependent variable scenarios. It effectively addresses cases where observations fall below or above a certain threshold, allowing for more accurate predictions in fields like econometrics and health economics. Explore the rest of the article to understand how the Tobit model can enhance your data analysis.
Table of Comparison
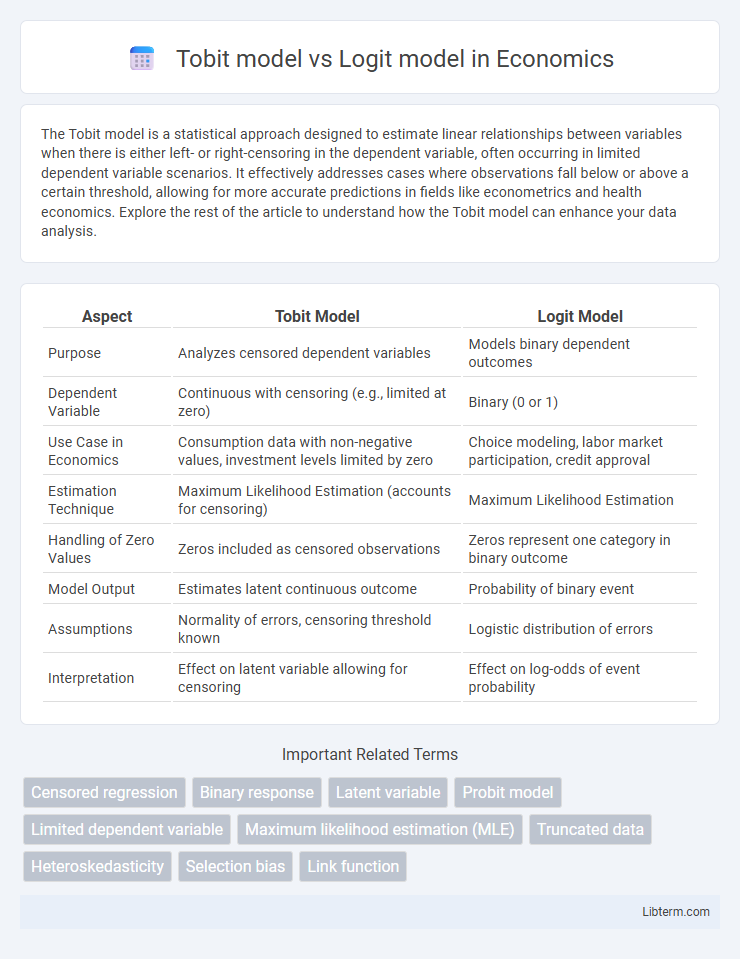
| Aspect | Tobit Model | Logit Model |
|---|---|---|
| Purpose | Analyzes censored dependent variables | Models binary dependent outcomes |
| Dependent Variable | Continuous with censoring (e.g., limited at zero) | Binary (0 or 1) |
| Use Case in Economics | Consumption data with non-negative values, investment levels limited by zero | Choice modeling, labor market participation, credit approval |
| Estimation Technique | Maximum Likelihood Estimation (accounts for censoring) | Maximum Likelihood Estimation |
| Handling of Zero Values | Zeros included as censored observations | Zeros represent one category in binary outcome |
| Model Output | Estimates latent continuous outcome | Probability of binary event |
| Assumptions | Normality of errors, censoring threshold known | Logistic distribution of errors |
| Interpretation | Effect on latent variable allowing for censoring | Effect on log-odds of event probability |
Introduction to Tobit and Logit Models
The Tobit model addresses censored dependent variables where observations are limited or truncated, making it ideal for analyzing outcomes with a significant portion of values at a boundary, such as zero. The Logit model, used for binary outcome variables, estimates the probability of discrete events by modeling the log-odds as a linear function of predictor variables. Tobit is employed in scenarios with continuous but censored data, while Logit focuses on classification with dichotomous responses.
Theoretical Foundations of Tobit Model
The Tobit model is grounded in the concept of censored regression, designed to handle dependent variables that are constrained or censored at a certain value, typically zero, reflecting limited dependent variables. It incorporates a latent variable framework where the observed outcome is only partially visible, capturing both the probability of being censored and the intensity of the outcome when not censored. This contrasts with the Logit model, which is based on logistic regression theory and focuses solely on modeling binary outcomes without accounting for censored or truncated data.
Theoretical Foundations of Logit Model
The Logit model is grounded in the theory of random utility maximization and assumes a logistic distribution of the error term, enabling it to model binary dependent variables effectively. It estimates the probability of an event occurring by transforming linear combinations of explanatory variables through the logistic function. This approach provides interpretable odds ratios and is widely applied in fields such as economics, epidemiology, and social sciences for discrete choice modeling.
Key Differences Between Tobit and Logit Models
Tobit and Logit models serve distinct purposes in statistical analysis, with Tobit models designed for censored dependent variables, often used when data is truncated or limited, such as expenditure data with zeros. Logit models, on the other hand, are applied for binary outcome variables, estimating the probability of a categorical response like success/failure or yes/no decisions. Key differences include Tobit's ability to handle continuous yet censored data through a latent variable framework, while Logit strictly models discrete, binary outcomes using logistic regression.
Applications of Tobit Model in Econometrics
The Tobit model is extensively used in econometrics to analyze censored dependent variables, such as household expenditure on durable goods or labor supply where the variable is limited by a threshold (e.g., zero). Unlike the Logit model, which is suitable for binary or categorical outcomes, the Tobit model effectively captures situations with continuous outcomes that are only observed within certain bounds, allowing for more accurate estimation of latent variables. Applications include modeling consumer demand, credit rationing, and investment decisions where data censoring or truncation is prevalent.
Applications of Logit Model in Econometrics
The Logit model, widely used in econometrics, excels in binary outcome prediction such as credit approval, labor market participation, and consumer choice analysis. Unlike the Tobit model, which handles censored dependent variables, the Logit model specifically estimates probabilities of discrete outcomes based on explanatory variables. Applications include assessing determinants of employment status, predicting consumer purchase decisions, and evaluating policy impacts on binary responses.
Assumptions Underlying Tobit and Logit Models
The Tobit model assumes a censored dependent variable where observations are only partially observed at certain limits, typically zero, and it requires normally distributed error terms with homoscedasticity. The Logit model assumes a binary dependent variable with outcomes following a logistic distribution and relies on the independence of irrelevant alternatives and no perfect multicollinearity among predictors. Tobit handles continuous and censored outcomes, while Logit is suited for discrete choice data without censoring.
Model Estimation: Tobit vs. Logit
The Tobit model estimates relationships when the dependent variable is censored, combining linear regression with probability modeling to handle left or right truncation in data. The Logit model estimates the probability of a binary outcome using maximum likelihood estimation, focusing on classification between two discrete states. Tobit is preferred for continuous outcomes with censoring, while Logit is suited for binary dependent variables without censoring constraints.
Interpreting Results from Tobit and Logit Models
Interpreting results from Tobit and Logit models requires understanding their respective data structures and outcome types. The Tobit model is suited for censored dependent variables and estimates both the probability of being above or below a threshold and the expected value conditional on being uncensored, providing coefficients that reflect latent variable impacts. In contrast, the Logit model handles binary outcomes by estimating the odds ratios, making it ideal for interpreting the likelihood of occurrence events, with coefficients indicating changes in log-odds associated with predictor variables.
Choosing Between Tobit and Logit Models: Practical Considerations
The Tobit model is ideal for analyzing censored dependent variables where outcomes are only observed within a certain range, such as expenditure data with many zero observations, while the Logit model suits binary outcome variables representing occurrence or non-occurrence of an event. Choosing between these models depends on the data structure: if the dependent variable is continuous but censored, Tobit accounts for the cumulative distribution below a threshold, whereas Logit models the probability of a categorical response. Practical considerations include the nature of the dependent variable, presence of censoring, and the research objective, with Tobit models providing estimates of both likelihood and intensity, and Logit models focusing solely on event probability.
Tobit model Infographic
 libterm.com
libterm.com