State price density represents the value today of a one-unit payoff in a future state, reflecting the probability-weighted discounted cash flows under risk-neutral valuation. It plays a crucial role in financial economics by helping to price contingent claims and derivatives accurately. Explore the rest of the article to understand how state price density impacts your investment decisions and asset pricing models.
Table of Comparison
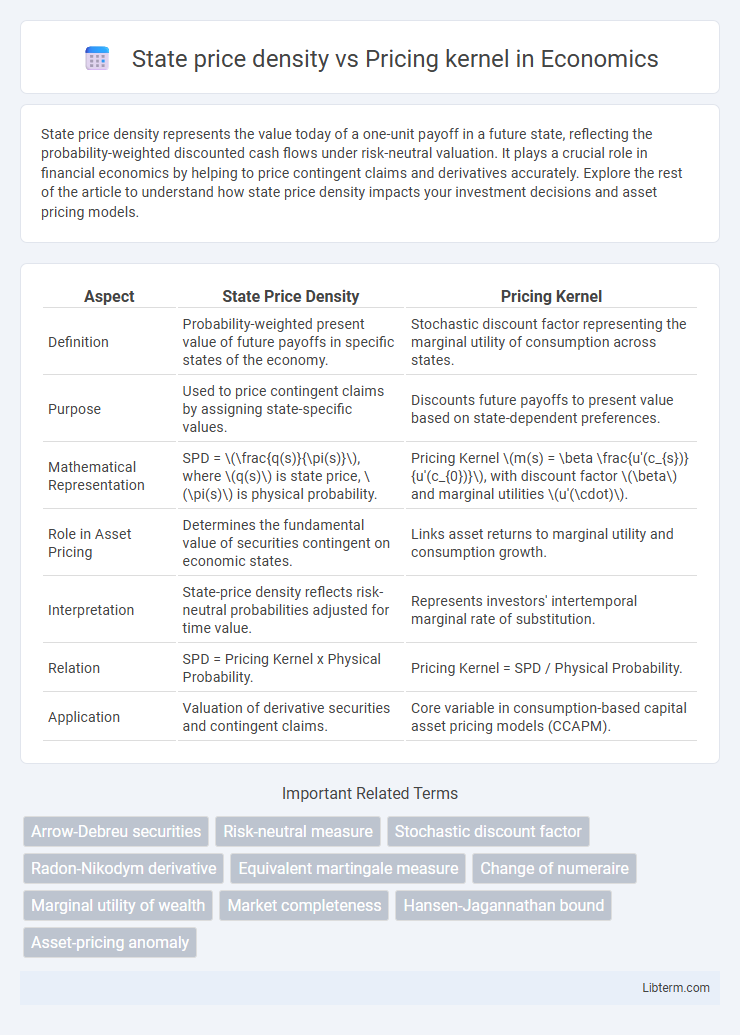
| Aspect | State Price Density | Pricing Kernel |
|---|---|---|
| Definition | Probability-weighted present value of future payoffs in specific states of the economy. | Stochastic discount factor representing the marginal utility of consumption across states. |
| Purpose | Used to price contingent claims by assigning state-specific values. | Discounts future payoffs to present value based on state-dependent preferences. |
| Mathematical Representation | SPD = \(\frac{q(s)}{\pi(s)}\), where \(q(s)\) is state price, \(\pi(s)\) is physical probability. | Pricing Kernel \(m(s) = \beta \frac{u'(c_{s})}{u'(c_{0})}\), with discount factor \(\beta\) and marginal utilities \(u'(\cdot)\). |
| Role in Asset Pricing | Determines the fundamental value of securities contingent on economic states. | Links asset returns to marginal utility and consumption growth. |
| Interpretation | State-price density reflects risk-neutral probabilities adjusted for time value. | Represents investors' intertemporal marginal rate of substitution. |
| Relation | SPD = Pricing Kernel x Physical Probability. | Pricing Kernel = SPD / Physical Probability. |
| Application | Valuation of derivative securities and contingent claims. | Core variable in consumption-based capital asset pricing models (CCAPM). |
Introduction to State Price Density and Pricing Kernel
State price density represents the price today of a future payoff in a specific state of the world, reflecting the market value assigned to each possible outcome. The pricing kernel, also known as the stochastic discount factor, is a fundamental concept that weights these future state-contingent payoffs by their marginal utility, bridging preferences and asset prices. Together, state price density and pricing kernel provide essential frameworks for understanding asset valuation under uncertainty and investor risk preferences.
Fundamental Concepts in Asset Pricing
State price density represents the present value of one unit of payoff in a specific future state, serving as a foundational concept in asset pricing to evaluate contingent claims. Pricing kernel, also known as the stochastic discount factor, captures an investor's marginal utility of consumption across different states, linking risk preferences with price formation in financial markets. Both concepts are intrinsically related by their role in discounting future payoffs but differ in interpretation: state price density reflects prices of state-contingent claims, while pricing kernel incorporates investor behavior and marginal utility adjustments.
Mathematical Definition of State Price Density
State price density, also known as the Radon-Nikodym derivative of the risk-neutral measure with respect to the real-world probability measure, provides the discounted prices of state-contingent claims in a financial market. Mathematically, it is defined as the ratio \( \frac{dQ}{dP} \frac{1}{B(t)} \), where \( Q \) is the risk-neutral measure, \( P \) the physical measure, and \( B(t) \) the discount factor. The pricing kernel, or stochastic discount factor, connects asset payoffs to their current prices by acting as a positive martingale under the physical measure, with the state price density being its formal representation in measure-theoretic terms.
Understanding the Pricing Kernel
The pricing kernel represents the state price density adjusted for probabilities, serving as a fundamental tool in asset pricing to determine the present value of uncertain future payoffs under risk-neutral measures. It quantifies the marginal utility of consumption across different states, linking investors' preferences with market prices of risk. Understanding the pricing kernel facilitates better insights into market equilibrium, risk aversion, and the stochastic discount factors driving asset returns.
Relationship Between State Price Density and Pricing Kernel
The state price density (SPD) and pricing kernel both represent essential tools for asset pricing in financial economics, where the SPD measures the price today of a unit payoff in a particular future state, while the pricing kernel denotes the stochastic discount factor reflecting marginal utility of consumption across states. The relationship between SPD and pricing kernel is mathematically expressed as the SPD being the product of the pricing kernel and the physical probability measure of future states. This linkage allows the transformation of physical probabilities into risk-neutral probabilities, enabling risk-adjusted valuation of contingent claims in incomplete markets.
Economic Interpretation and Insights
State price density represents the discounted probability distribution of future states, reflecting how much investors are willing to pay today for payoffs in different states of the world. The pricing kernel, or stochastic discount factor, captures the marginal utility of consumption and serves as a fundamental tool in asset pricing by adjusting future payoffs for time and risk preferences. Economic interpretation reveals that while state price density links directly to market prices and risk-neutral probabilities, the pricing kernel conveys investors' risk aversion and consumption-smoothing behavior, providing deeper insights into risk pricing and intertemporal consumption decisions.
Applications in Financial Modeling
State price density, also called Arrow-Debreu prices, represents the discounted probability of future states in asset pricing and is fundamental in calculating the present value of contingent claims. The pricing kernel, or stochastic discount factor, adjusts payoffs for risk preferences and time value, serving as a key tool to link asset prices with macroeconomic factors. In financial modeling, state price density is crucial for option pricing and risk-neutral valuation, while pricing kernels enable the assessment of risk premia and the derivation of equilibrium asset prices under varying economic scenarios.
Estimation Methods and Techniques
State price density (SPD) and pricing kernel estimation methods primarily rely on nonparametric and parametric approaches derived from option prices and asset returns. Techniques such as Breeden-Litzenberger's second derivative method extract SPD directly from option price data, while kernel smoothing and local polynomial regression enhance estimation accuracy in noisy markets. Advanced methods involve maximum likelihood estimation and Bayesian inference to estimate the pricing kernel, capturing investors' risk preferences and improving asset pricing model calibration.
Empirical Evidence and Case Studies
Empirical evidence comparing state price densities and pricing kernels reveals that both concepts serve as fundamental tools in asset pricing, with state price densities representing the market's valuation of future states and pricing kernels reflecting marginal utility weights. Case studies, such as those involving equity markets and bond pricing, demonstrate that pricing kernels derived from consumption-based models often capture investor risk preferences more accurately, whereas state price densities provide direct insights into market-implied probabilities and risk-neutral valuations. Empirical estimations using option data and consumption growth further highlight the strengths and limitations of each approach in explaining observed asset prices across different economic conditions.
Implications for Risk Management and Derivative Pricing
State price density, representing the price today of a unit payoff in a future state, plays a crucial role in derivative pricing by directly linking current market prices to possible future outcomes. The pricing kernel, or stochastic discount factor, adjusts for risk preferences and time value of money, enabling more accurate risk-neutral valuation of assets and derivatives. Understanding the relationship between state price density and the pricing kernel allows risk managers to better hedge against market uncertainties and price complex financial instruments with enhanced precision.
State price density Infographic
 libterm.com
libterm.com