The Stirling cycle is a thermodynamic process used in Stirling engines, which operate by cyclic compression and expansion of air or other gases at different temperature levels, converting heat energy into mechanical work. This efficiency and quiet operation make it ideal for applications in renewable energy and low-emission power generation. Explore the rest of the article to understand how the Stirling cycle can optimize your energy systems.
Table of Comparison
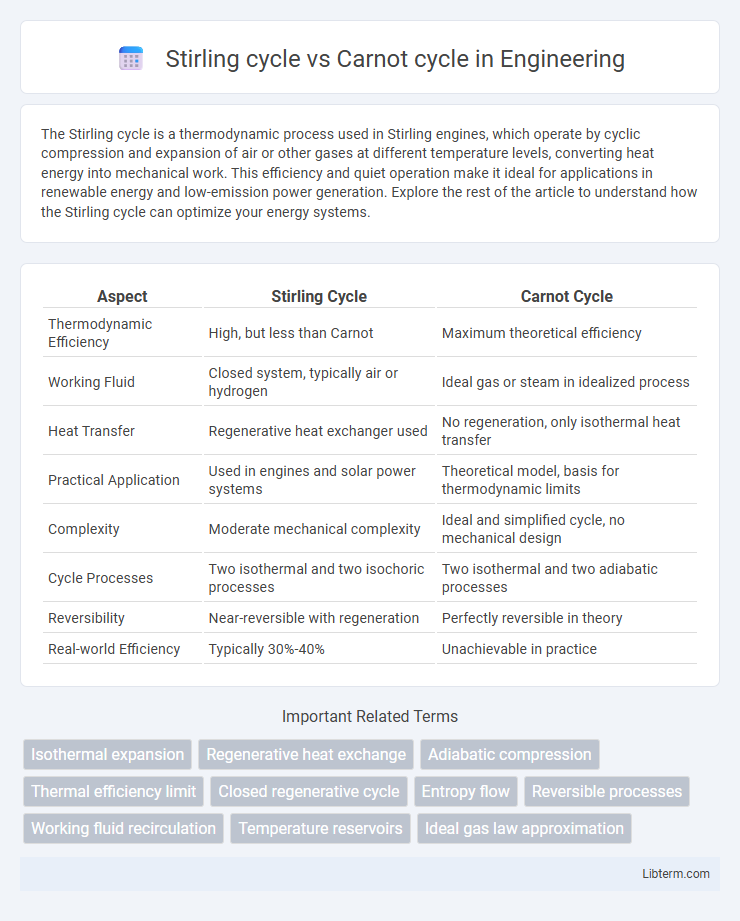
| Aspect | Stirling Cycle | Carnot Cycle |
|---|---|---|
| Thermodynamic Efficiency | High, but less than Carnot | Maximum theoretical efficiency |
| Working Fluid | Closed system, typically air or hydrogen | Ideal gas or steam in idealized process |
| Heat Transfer | Regenerative heat exchanger used | No regeneration, only isothermal heat transfer |
| Practical Application | Used in engines and solar power systems | Theoretical model, basis for thermodynamic limits |
| Complexity | Moderate mechanical complexity | Ideal and simplified cycle, no mechanical design |
| Cycle Processes | Two isothermal and two isochoric processes | Two isothermal and two adiabatic processes |
| Reversibility | Near-reversible with regeneration | Perfectly reversible in theory |
| Real-world Efficiency | Typically 30%-40% | Unachievable in practice |
Introduction to Thermodynamic Cycles
The Stirling cycle operates on a closed regenerative thermodynamic process involving isothermal expansion and compression coupled with constant-volume heat transfer, achieving high efficiency through external heat addition. The Carnot cycle represents an idealized reversible cycle consisting of two isothermal and two adiabatic processes, establishing the maximum theoretical efficiency limit for heat engines between two thermal reservoirs. Both cycles provide fundamental models for analyzing thermodynamic efficiency, with the Carnot cycle serving as a benchmark and the Stirling cycle exemplifying practical regenerative heat engine design.
Overview of the Stirling Cycle
The Stirling cycle is a closed-cycle regenerative heat engine that operates with a fixed amount of working gas, converting thermal energy into mechanical work through cyclic compression and expansion at different temperature levels. Unlike the Carnot cycle, which is theoretical and idealized with isothermal and adiabatic processes, the Stirling cycle includes two isothermal processes and two constant-volume regenerative heat exchange processes, enhancing efficiency. This cycle's practical design allows for high thermal efficiency closer to the Carnot limit, especially when equipped with an effective regenerator that minimizes heat loss between the hot and cold reservoirs.
Fundamentals of the Carnot Cycle
The Carnot cycle operates on two isothermal processes and two adiabatic processes, representing an idealized heat engine with maximum efficiency determined solely by the temperature difference between the heat source and sink. Its fundamental principle is reversible operation, ensuring zero entropy generation and maximum work output. In contrast, the Stirling cycle, though also reversible, consists of two isothermal and two isochoric processes, emphasizing practical efficiency through external regeneration but typically achieving lower theoretical efficiency than the Carnot cycle.
Key Differences Between Stirling and Carnot Cycles
The Stirling cycle operates through isothermal expansion and compression with constant volume regeneration, while the Carnot cycle consists of isothermal and adiabatic processes without regeneration. Stirling engines utilize external heat sources and a regenerator to improve efficiency, whereas Carnot engines are idealized models focused on maximum theoretical efficiency between two thermal reservoirs. Efficiency in the Carnot cycle depends solely on temperature difference, while Stirling cycle efficiency is influenced by practical factors like regenerator effectiveness and mechanical simplicity.
Thermodynamic Efficiency Comparison
The Stirling cycle achieves high thermodynamic efficiency by utilizing isothermal expansion and compression processes, closely approaching the theoretical maximum efficiency defined by the Carnot cycle. While the Carnot cycle represents the idealized benchmark with maximum possible efficiency between two temperature reservoirs, practical limitations such as finite heat transfer rates and regenerative losses reduce the Stirling engine's real-world performance. Nonetheless, the Stirling cycle often surpasses typical internal combustion engines by maintaining efficiencies up to 40-50%, whereas the Carnot cycle sets an upper bound based solely on reservoir temperatures.
Real-World Applications of Stirling and Carnot Cycles
The Carnot cycle, representing an idealized thermodynamic process with maximum efficiency, serves primarily as a theoretical benchmark for heat engine performance. Stirling engines, operating on a closed regenerative cycle, are widely utilized in real-world applications such as solar power generation, submarine propulsion, and cryogenic cooling due to their high efficiency and ability to run on various heat sources. Unlike the Carnot cycle, Stirling engines offer practical advantages including lower emissions and quiet operation, making them suitable for renewable energy systems and environmentally friendly industrial uses.
Advantages and Disadvantages of the Stirling Cycle
The Stirling cycle offers higher thermal efficiency compared to typical internal combustion engines due to its closed-cycle operation and external heat source, enabling fuel flexibility and lower emissions. Its disadvantages include complex heat exchanger designs and slower dynamic response, limiting its application in high-power, rapidly changing load environments. While the Carnot cycle represents the ideal maximum efficiency in theoretical thermodynamics, the Stirling cycle provides a more practical and implementable balance of efficiency and operational feasibility in real-world engines.
Advantages and Disadvantages of the Carnot Cycle
The Carnot cycle offers the highest theoretical efficiency between two temperature reservoirs, making it the ideal benchmark for heat engine performance. Its reversible processes minimize entropy generation, ensuring maximum work output for a given heat input. However, the Carnot cycle is impractical for real-world applications due to its requirement for infinitely slow processes, perfect insulation, and idealized components, resulting in low power density and complex operational demands.
Practical Considerations in Engine Design
The Stirling cycle offers higher practical efficiency and smoother operation due to continuous external combustion and regenerative heat exchange, reducing thermal losses compared to the Carnot cycle's theoretical maximum efficiency with idealized reversible processes. Stirling engines are favored in engine design for their ability to use various heat sources and lower mechanical complexity, whereas Carnot engines remain mostly a benchmark without practical implementation. Material limitations, heat transfer rates, and real-world irreversibilities make the Stirling cycle a more viable option for efficient and reliable engine performance.
Future Trends in Thermodynamic Cycle Research
Future trends in thermodynamic cycle research emphasize enhancing the efficiency and sustainability of Stirling and Carnot cycles through advanced materials and integration with renewable energy systems. Innovations in micro-scale Stirling engines and hybrid Carnot-Stirling configurations aim to reduce irreversibilities and improve real-world thermal performance. Computational modeling and AI-driven optimization techniques are increasingly applied to design cycles that maximize work output while minimizing environmental impact.
Stirling cycle Infographic
 libterm.com
libterm.com