The finite difference method approximates solutions to differential equations by replacing derivatives with difference equations on discrete grid points. This numerical technique is widely used in engineering and physics to model heat transfer, fluid dynamics, and more. Dive into the rest of the article to explore how this method can enhance your computational problem-solving skills.
Table of Comparison
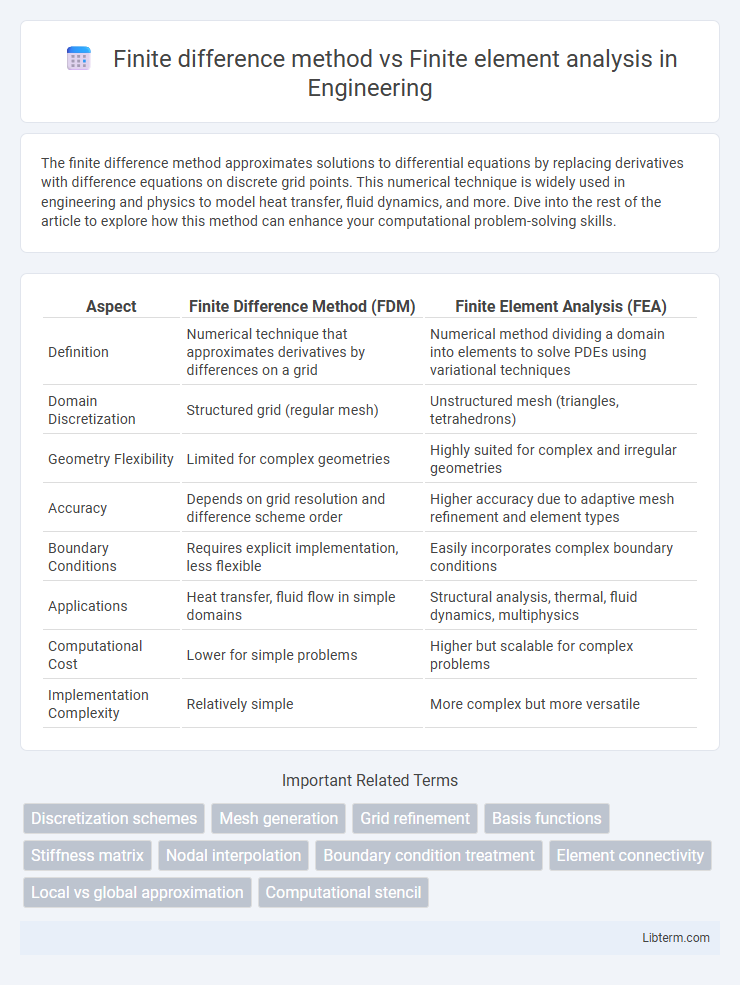
| Aspect | Finite Difference Method (FDM) | Finite Element Analysis (FEA) |
|---|---|---|
| Definition | Numerical technique that approximates derivatives by differences on a grid | Numerical method dividing a domain into elements to solve PDEs using variational techniques |
| Domain Discretization | Structured grid (regular mesh) | Unstructured mesh (triangles, tetrahedrons) |
| Geometry Flexibility | Limited for complex geometries | Highly suited for complex and irregular geometries |
| Accuracy | Depends on grid resolution and difference scheme order | Higher accuracy due to adaptive mesh refinement and element types |
| Boundary Conditions | Requires explicit implementation, less flexible | Easily incorporates complex boundary conditions |
| Applications | Heat transfer, fluid flow in simple domains | Structural analysis, thermal, fluid dynamics, multiphysics |
| Computational Cost | Lower for simple problems | Higher but scalable for complex problems |
| Implementation Complexity | Relatively simple | More complex but more versatile |
Introduction to Numerical Methods in Engineering
The finite difference method (FDM) and finite element analysis (FEA) are fundamental numerical techniques in engineering for solving differential equations and boundary value problems. FDM discretizes the domain into a grid and approximates derivatives using difference equations, making it well-suited for problems with simple geometries and structured meshes. FEA divides the domain into smaller, complex elements and applies variational methods to achieve higher accuracy for irregular geometries and complex boundary conditions, often used in structural and thermal analysis.
Overview of Finite Difference Method (FDM)
Finite Difference Method (FDM) approximates differential equations by replacing derivatives with difference equations on a discrete grid, enabling numerical solutions for partial differential equations common in heat transfer and fluid dynamics. The method's simplicity and ease of implementation make it ideal for structured grids and problems with regular geometries, though it struggles with complex boundaries compared to Finite Element Analysis (FEA). FDM emphasizes local error minimization through Taylor series expansion, providing straightforward discretization but limited flexibility in handling irregular meshes or adaptive refinement.
Overview of Finite Element Analysis (FEA)
Finite Element Analysis (FEA) is a computational technique used to approximate solutions for complex engineering problems by breaking down a large system into smaller, simpler finite elements. Unlike the Finite Difference Method, which focuses on discretizing differential equations over a grid, FEA uses variational methods to minimize an energy function and provides high accuracy in structural, thermal, and fluid dynamics simulations. It is widely applied in industries such as aerospace, automotive, and biomechanics for stress analysis, deformation prediction, and optimizing material properties.
Mathematical Foundations: FDM vs FEA
Finite Difference Method (FDM) relies on discretizing partial differential equations by approximating derivatives via differences on structured grids, enabling straightforward numerical solutions. Finite Element Analysis (FEA) utilizes variational principles and weak formulations to transform differential equations into integral equations over subdivided finite elements, accommodating complex geometries and boundary conditions. The mathematical foundation of FDM centers on Taylor series expansions for derivative approximations, while FEA is grounded in functional analysis and Galerkin methods for solution approximation within defined function spaces.
Discretization Techniques Compared
Finite difference method discretizes the domain by dividing it into a structured grid of evenly spaced nodes, approximating derivatives using difference equations at these points. Finite element analysis partitions the domain into unstructured elements of varying shapes and sizes, employing piecewise polynomial shape functions for interpolation within each element. The flexibility of element shapes in finite elements allows for more accurate modeling of complex geometries compared to the regular grid used in finite difference methods.
Application Areas of FDM and FEA
Finite difference method (FDM) is widely applied in fields like heat transfer, fluid dynamics, and financial modeling due to its straightforward approach to solving partial differential equations on structured grids. Finite element analysis (FEA) excels in structural engineering, biomechanics, and automotive design by handling complex geometries and material behaviors with unstructured meshes. While FDM suits problems with simple domains and regular boundaries, FEA is preferred for simulations requiring detailed stress analysis and heterogeneous material properties.
Accuracy and Convergence Analysis
Finite difference method (FDM) offers straightforward implementation and clear error estimation but may struggle with complex geometries affecting accuracy, while finite element analysis (FEA) excels in handling irregular domains with higher precision. Convergence analysis in FDM depends heavily on mesh uniformity and step size, often requiring smaller grid spacing for stability, whereas FEA achieves convergence through adaptive mesh refinement and higher-order shape functions. Studies confirm that FEA generally provides superior accuracy and robust convergence for complex boundary conditions compared to traditional FDM approaches.
Computational Efficiency and Resource Requirements
Finite difference method (FDM) generally offers higher computational efficiency for problems with simple geometries due to its straightforward grid-based approach and lower memory requirements. Finite element analysis (FEA) demands more computational resources because of complex mesh generation and solving large systems of equations, yet it excels in handling irregular geometries and boundary conditions. Optimizing resource allocation in FEA can leverage adaptive mesh refinement techniques, whereas FDM benefits from uniform grids but struggles with complex domain discretization.
Advantages and Limitations of Each Method
The finite difference method offers simplicity and ease of implementation for solving partial differential equations, particularly effective on structured grids but struggles with complex geometries and boundary conditions. Finite element analysis excels in handling intricate geometries and variable material properties through mesh flexibility and provides higher accuracy for stress analysis, but involves increased computational cost and complexity in mesh generation. Choosing between finite difference and finite element methods depends on the problem domain, required precision, and computational resources available.
Choosing Between FDM and FEA: Key Considerations
Choosing between Finite Difference Method (FDM) and Finite Element Analysis (FEA) depends on problem complexity and geometry; FDM excels in structured grids and simple boundary conditions, while FEA handles irregular domains and complex geometries more effectively. Computational resources and accuracy requirements also influence the decision, with FEA offering higher flexibility and precision for stress analysis, heat transfer, and fluid dynamics. Engineers must consider mesh adaptability, ease of implementation, and the specific application to determine the optimal numerical approach.
Finite difference method Infographic
 libterm.com
libterm.com