The transfer matrix is a powerful tool in physics and engineering used to analyze wave propagation, quantum systems, and electrical networks by representing system states and their transformations. It simplifies complex problems by breaking them down into a series of matrix multiplications, making it easier to model multilayer structures and signal transmission. Explore the details in the rest of the article to understand how the transfer matrix can optimize your problem-solving approach.
Table of Comparison
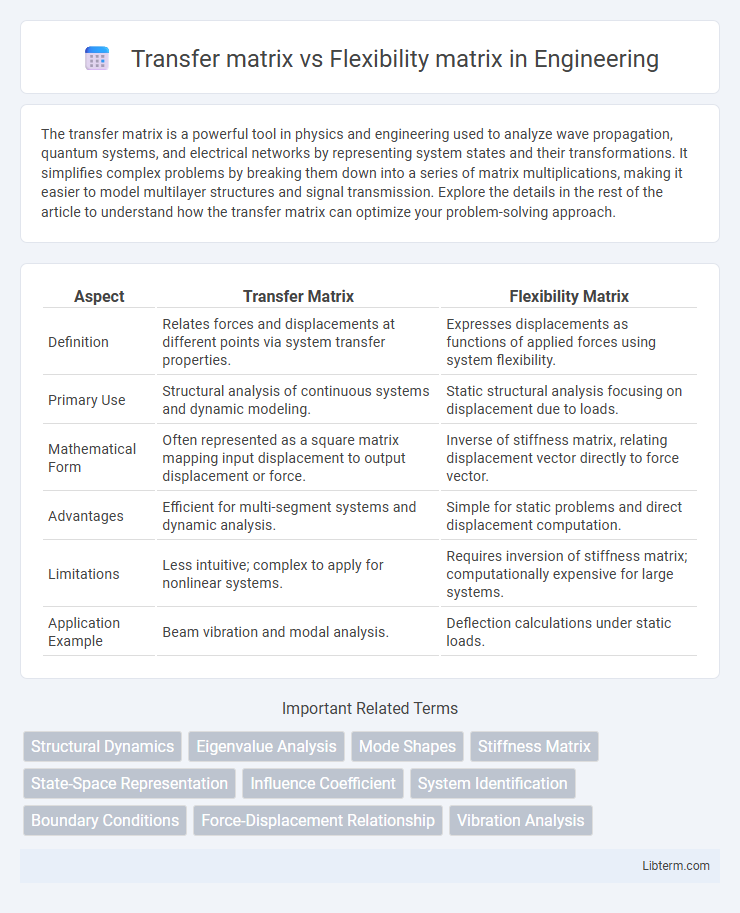
| Aspect | Transfer Matrix | Flexibility Matrix |
|---|---|---|
| Definition | Relates forces and displacements at different points via system transfer properties. | Expresses displacements as functions of applied forces using system flexibility. |
| Primary Use | Structural analysis of continuous systems and dynamic modeling. | Static structural analysis focusing on displacement due to loads. |
| Mathematical Form | Often represented as a square matrix mapping input displacement to output displacement or force. | Inverse of stiffness matrix, relating displacement vector directly to force vector. |
| Advantages | Efficient for multi-segment systems and dynamic analysis. | Simple for static problems and direct displacement computation. |
| Limitations | Less intuitive; complex to apply for nonlinear systems. | Requires inversion of stiffness matrix; computationally expensive for large systems. |
| Application Example | Beam vibration and modal analysis. | Deflection calculations under static loads. |
Introduction to Structural Analysis Matrices
The transfer matrix and flexibility matrix are fundamental tools in structural analysis matrices, used to determine the behavior of structures under loads. The transfer matrix relates state vectors at different points in a structure, facilitating dynamic analysis and stability evaluation, while the flexibility matrix represents the displacement response of a structure to applied forces, enabling static deflection calculations. Understanding these matrices is essential for accurate modeling and analysis of structural systems in engineering applications.
What is a Transfer Matrix?
A Transfer Matrix is a mathematical representation used in structural engineering to analyze the relationship between forces and displacements in a system by transferring state variables from one section to another. It simplifies complex structural analysis by breaking down structures into smaller segments, enabling the calculation of overall responses through matrix multiplication. Unlike the Flexibility Matrix, which directly relates applied loads to displacements, the Transfer Matrix focuses on the propagation of state vectors along the structure.
What is a Flexibility Matrix?
A Flexibility Matrix is a fundamental concept in structural engineering representing the inverse of the stiffness matrix, used to relate applied forces to resultant displacements in a system. It quantifies the flexibility of structures by expressing how much deformation occurs under specific loads, enabling engineers to analyze structural behavior in static analysis. Unlike the Transfer Matrix, which maps state variables between different sections of a system, the Flexibility Matrix directly provides displacement responses to applied forces, making it essential for flexibility method formulations.
Mathematical Formulation of Transfer Matrix
The transfer matrix method involves expressing the relationship between state vectors at two points in a structure using a matrix that encapsulates system parameters, boundary conditions, and load effects. Mathematically, the transfer matrix \( T \) relates the state vector \( \mathbf{x}_1 \) at one section to \( \mathbf{x}_2 \) at another via \( \mathbf{x}_2 = T \mathbf{x}_1 \), where \( T \) comprises stiffness, mass, and damping coefficients depending on the mechanical system. This formulation contrasts with the flexibility matrix approach, which directly relates applied forces to displacements through an inverse stiffness operator, while the transfer matrix method focuses on propagating state variables along the structure.
Mathematical Representation of Flexibility Matrix
The flexibility matrix in structural analysis is mathematically represented as the inverse of the stiffness matrix, expressing displacements as functions of applied forces. Unlike the transfer matrix, which describes state changes between adjacent structural elements through propagation of forces and displacements, the flexibility matrix directly quantifies displacement responses to unit loads, enabling calculation of deformations under given external forces. Its entries consist of flexibility coefficients, each representing the displacement in a degree of freedom due to a unit load applied at another degree of freedom, forming a symmetric and positive definite matrix in linear elastic systems.
Key Differences Between Transfer and Flexibility Matrices
The transfer matrix relates forces and displacements at different points in a structural system, focusing on how input forces cause output displacements, often used in structural dynamics and control. The flexibility matrix, on the other hand, directly links applied forces to resulting displacements within the same points, emphasizing material and geometric compliance characteristics. Key differences lie in their applications: transfer matrices facilitate system-level behavior modeling and control, while flexibility matrices provide detailed deformation analysis for structural components.
Applications in Structural Engineering
The transfer matrix method is extensively used for analyzing multi-degree-of-freedom structural systems by relating displacement and force vectors across elements, enabling efficient computation of deflections and internal forces. The flexibility matrix approach provides direct insight into structural compliance by expressing displacements as functions of applied loads, making it valuable for analyzing indeterminate structures and assessing deformation patterns. Both methods facilitate structural design optimization, but the transfer matrix is preferred for dynamic analysis and stability studies, while the flexibility matrix is advantageous in static load-response evaluations.
Advantages and Limitations of Each Matrix
The transfer matrix offers advantages in structural analysis by providing a straightforward method to relate forces and displacements across structural elements, enabling efficient modeling of continuous systems. However, it can become complex and less practical for large systems due to the multiplication of numerous matrices, which may lead to numerical instability. The flexibility matrix excels in evaluating indeterminate structures by expressing displacements as functions of applied forces and is beneficial for analyzing static systems, but it requires prior knowledge of the system's flexibility coefficients and can be computationally intensive for structures with many degrees of freedom.
Comparison Table: Transfer Matrix vs Flexibility Matrix
The transfer matrix and flexibility matrix are fundamental tools in structural analysis, with the transfer matrix relating nodal displacements and forces through element stiffness properties, while the flexibility matrix expresses displacements directly as functions of applied forces. Transfer matrices suit dynamic and multi-degree-of-freedom systems by enabling recursive system assembly, whereas flexibility matrices are more intuitive for statically determinate systems and direct displacement calculations. The comparison table highlights differences: transfer matrices focus on stiffness representation with multiplicative state vector transformations, flexibility matrices emphasize compliance with inverse stiffness representation, and computational efficiency varies depending on system complexity and analysis type.
Choosing the Right Matrix for Analysis
Selecting the appropriate matrix for structural analysis hinges on the problem's complexity and boundary conditions; the transfer matrix efficiently handles discrete systems with clear state transitions, while the flexibility matrix excels in analyzing continuous systems and indeterminate structures by relating applied loads to displacements. Engineers prioritize the transfer matrix for dynamic analysis and multi-degree-of-freedom systems due to its computational efficiency, whereas the flexibility matrix is favored in static analysis with known load-deflection relationships. Understanding these distinctions ensures accurate, optimized modeling and solution strategies in structural mechanics and vibration analysis.
Transfer matrix Infographic
 libterm.com
libterm.com