Particle methods simulate physical systems by representing materials as discrete particles, enabling detailed modeling of fluid flows, granular materials, and solid mechanics. These techniques offer advantages in handling complex boundaries and large deformations that traditional grid-based approaches struggle with. Discover how particle methods can enhance your simulations by exploring the full article.
Table of Comparison
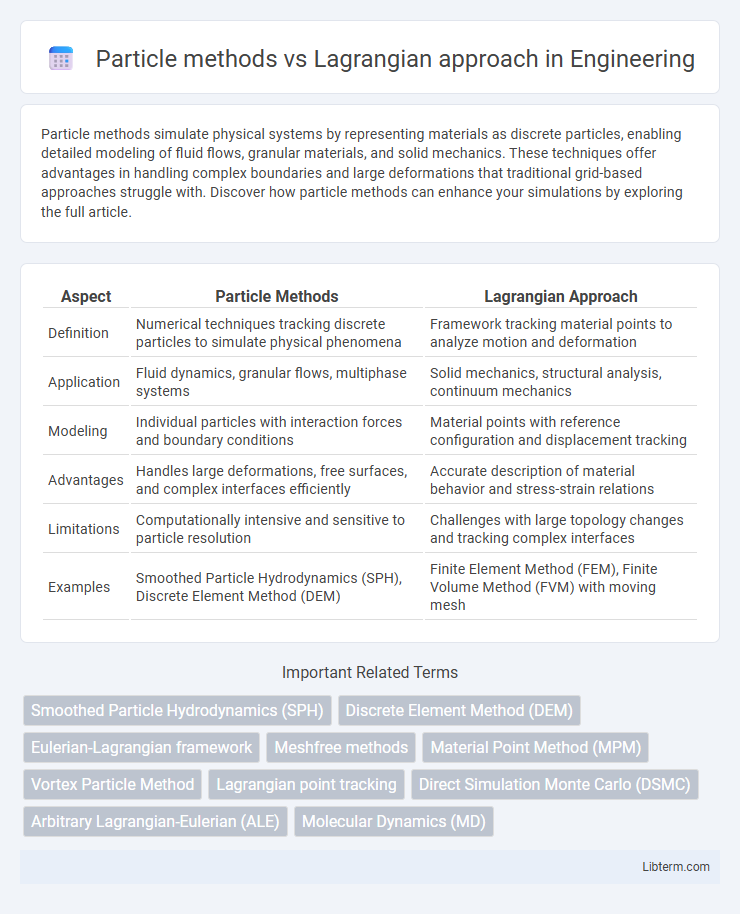
| Aspect | Particle Methods | Lagrangian Approach |
|---|---|---|
| Definition | Numerical techniques tracking discrete particles to simulate physical phenomena | Framework tracking material points to analyze motion and deformation |
| Application | Fluid dynamics, granular flows, multiphase systems | Solid mechanics, structural analysis, continuum mechanics |
| Modeling | Individual particles with interaction forces and boundary conditions | Material points with reference configuration and displacement tracking |
| Advantages | Handles large deformations, free surfaces, and complex interfaces efficiently | Accurate description of material behavior and stress-strain relations |
| Limitations | Computationally intensive and sensitive to particle resolution | Challenges with large topology changes and tracking complex interfaces |
| Examples | Smoothed Particle Hydrodynamics (SPH), Discrete Element Method (DEM) | Finite Element Method (FEM), Finite Volume Method (FVM) with moving mesh |
Introduction to Particle Methods and Lagrangian Approaches
Particle methods represent numerical techniques that simulate fluid or solid dynamics by tracking discrete particles, allowing for detailed modeling of complex interfaces and free-surface flows. The Lagrangian approach follows individual particles or material points as they move through space and time, providing a natural framework for capturing deformation and transport phenomena with minimal numerical diffusion. Combining particle methods with the Lagrangian perspective enhances accuracy in multiphase flow simulations and improves the handling of large deformations in computational mechanics.
Fundamental Principles of Particle Methods
Particle methods represent physical systems through discrete particles that carry properties such as mass, velocity, and position, enabling the simulation of complex phenomena like fluid flow and solid deformation. These methods rely on the Lagrangian approach, tracking individual particles as they move through space and time, preserving material interfaces and capturing large deformations without mesh distortion. Fundamental principles include the discretization of continuum fields into particles, interpolation of field quantities using kernel functions, and the integration of governing equations directly on particle positions, which distinguishes particle methods from traditional Eulerian grid-based techniques.
Core Concepts of the Lagrangian Approach
The Lagrangian approach tracks individual fluid particles by following their trajectories through space and time, providing detailed insight into particle dynamics and deformation. This method emphasizes solving equations of motion based on particle positions, velocities, and forces, enabling accurate modeling of complex flow behaviors such as turbulence and multiphase interactions. Core concepts include material derivatives, particle tracking, and the transformation between reference and current configurations to capture fluid motion non-intrusively.
Key Differences Between Particle and Lagrangian Methods
Particle methods track individual particles through time, emphasizing discrete elements in fluid or solid simulations, whereas the Lagrangian approach follows material points moving with the flow to analyze deformation and displacement. Particle methods excel in handling large deformations and complex boundary interactions, while Lagrangian techniques provide detailed descriptions of continuum mechanics in a moving reference frame. The key differences lie in representation granularity, computational flexibility, and application scope, with particle methods favoring mesh-free discretization and Lagrangian approaches relying on mesh-based tracking of material geometry.
Applications of Particle Methods in Physics and Engineering
Particle methods, such as Smoothed Particle Hydrodynamics (SPH) and Discrete Element Method (DEM), excel in simulating fluid dynamics, granular flows, and multiphase systems by representing media as discrete particles following Newtonian mechanics. These methods enable accurate modeling of complex phenomena like free-surface flows, fracture dynamics, and powder behavior in engineering processes, where mesh-based techniques face limitations. Applications span astrophysics, biomechanics, and civil engineering, providing robust tools for analyzing particle interactions and material deformations under diverse conditions.
Typical Uses of Lagrangian Approaches
Lagrangian approaches excel in fluid dynamics simulations, tracking individual particles or fluid parcels to analyze flow behavior, turbulence, and mixing processes with high precision. These methods are widely used in meteorology, oceanography, and combustion modeling, where understanding particle trajectories and interactions is crucial. The ability to capture detailed motion and deformation of materials makes Lagrangian approaches ideal for studying multiphase flows, sediment transport, and biomechanical systems.
Advantages and Limitations of Particle Methods
Particle methods offer significant advantages such as natural handling of complex free-surface flows, flexibility in tracking large deformations, and reduced numerical diffusion compared to grid-based approaches. Their Lagrangian framework allows direct representation of material points, improving accuracy in simulating multi-phase flows and interfaces, but challenges include high computational cost, difficulties in enforcing boundary conditions, and potential particle clustering or deficiency. Despite limitations, particle methods excel in problems involving fragmentation, mixing, and large topology changes that are cumbersome for traditional Lagrangian mesh-based methods.
Pros and Cons of the Lagrangian Approach
The Lagrangian approach tracks individual particles' trajectories, allowing precise modeling of complex fluid flows and interfaces, which enhances accuracy in simulations of multiphase systems. However, it can be computationally expensive and challenging to manage for large-scale problems due to the need for tracking numerous particles and handling particle interactions. Despite these limitations, the Lagrangian method excels in capturing detailed local dynamics and is highly effective in applications such as spray modeling and sediment transport.
Comparative Analysis: Efficiency and Accuracy
Particle methods excel in handling complex fluid dynamics by discretizing the domain into particles, offering high accuracy in simulating free surface flows and multiphase interactions. The Lagrangian approach tracks individual fluid parcels, providing precise trajectory information but often at higher computational costs due to mesh distortion and remeshing requirements. Comparative analysis reveals particle methods generally achieve greater efficiency and robustness in large deformation scenarios, while the Lagrangian approach maintains superior accuracy in small-scale, well-defined flow regimes.
Future Trends in Particle and Lagrangian Simulation Methods
Future trends in particle methods and Lagrangian simulation focus on enhancing computational efficiency and accuracy through hybrid techniques combining mesh-based and mesh-free approaches. Advances in machine learning integration aim to optimize particle interaction models and enable real-time adaptive simulations for complex fluid dynamics and multiphase flows. Research also prioritizes scalability on high-performance computing platforms to address large-scale environmental and engineering applications.
Particle methods Infographic
 libterm.com
libterm.com