The polar moment of inertia measures an object's ability to resist torsional deformation around an axis, crucial in designing shafts and structural components subjected to twisting forces. It quantifies how material is distributed about the axis of rotation, directly influencing the object's strength and stability under torque. Explore the rest of the article to understand how the polar moment of inertia impacts your engineering projects and material selection.
Table of Comparison
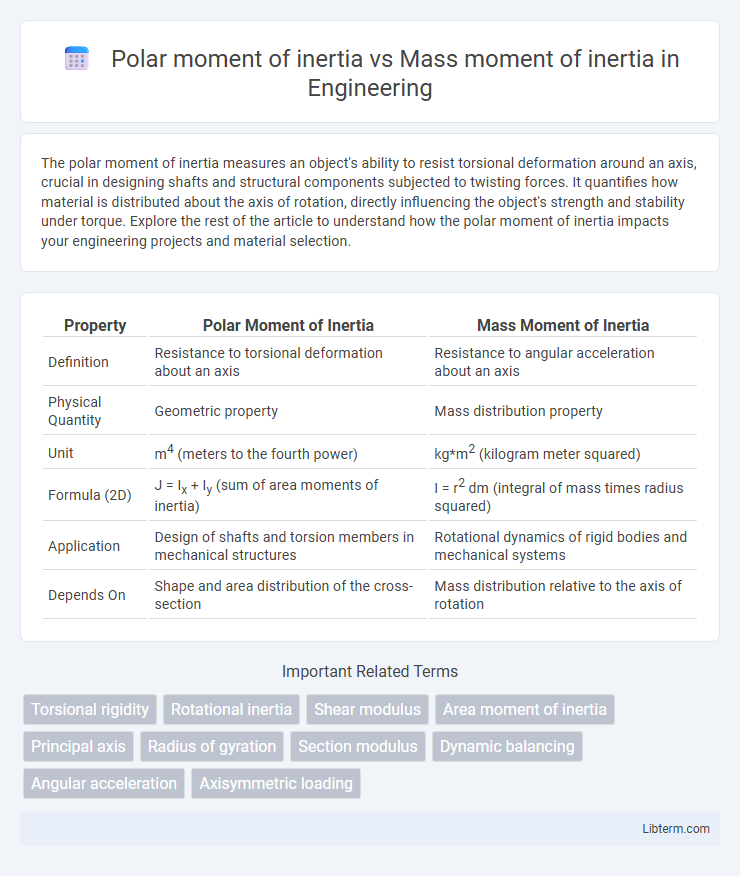
| Property | Polar Moment of Inertia | Mass Moment of Inertia |
|---|---|---|
| Definition | Resistance to torsional deformation about an axis | Resistance to angular acceleration about an axis |
| Physical Quantity | Geometric property | Mass distribution property |
| Unit | m4 (meters to the fourth power) | kg*m2 (kilogram meter squared) |
| Formula (2D) | J = Ix + Iy (sum of area moments of inertia) | I = r2 dm (integral of mass times radius squared) |
| Application | Design of shafts and torsion members in mechanical structures | Rotational dynamics of rigid bodies and mechanical systems |
| Depends On | Shape and area distribution of the cross-section | Mass distribution relative to the axis of rotation |
Introduction to Moment of Inertia
The polar moment of inertia quantifies an object's resistance to torsional deformation about an axis, reflecting the distribution of area in a plane perpendicular to that axis, while the mass moment of inertia measures resistance to angular acceleration based on mass distribution relative to the rotational axis. Both concepts are crucial in mechanical engineering and structural analysis for predicting dynamic behavior under rotational forces. Understanding the distinction between area-based polar moment of inertia and mass-based mass moment of inertia enables precise design and optimization of shafts, beams, and rotating machinery components.
Defining Polar Moment of Inertia
Polar moment of inertia measures an object's resistance to torsional deformation around a specific axis, focusing on the distribution of cross-sectional area relative to that axis. It is defined mathematically as the integral of the square of the radial distance from the axis times the differential area element, expressed in units such as meters to the fourth power (m4). Unlike mass moment of inertia, which accounts for mass distribution and resists angular acceleration, polar moment of inertia solely concerns geometric properties influencing torsion.
Explaining Mass Moment of Inertia
Mass moment of inertia quantifies an object's resistance to angular acceleration, depending on the distribution of mass relative to the axis of rotation. Unlike the polar moment of inertia which measures resistance to torsion or twisting in circular cross-sections, mass moment of inertia incorporates the entire mass distribution in three-dimensional space. It plays a critical role in dynamics and mechanical engineering by influencing rotational motion, stability, and energy requirements for rotating bodies.
Key Differences Between Polar and Mass Moment of Inertia
Polar moment of inertia quantifies an object's resistance to torsional deformation around an axis, calculated as the sum of squared distances of mass elements from that central axis, typically in circular cross-sections. Mass moment of inertia measures resistance to angular acceleration about a specific axis, dependent on mass distribution relative to that axis but applicable in bending and rotational contexts as well. The key difference lies in polar moment being used primarily for torsion analysis in shafts and circular bodies, while mass moment applies broadly in dynamics for any rotational axis and shape.
Mathematical Expressions and Units
The polar moment of inertia, denoted \(J\), is mathematically expressed as \(J = \int r^2 \, dA\), where \(r\) is the radial distance from the axis of rotation and \(dA\) represents an infinitesimal area element, with units in \(\text{m}^4\). The mass moment of inertia, represented as \(I\), is given by \(I = \int r^2 \, dm\), where \(dm\) is an infinitesimal mass element positioned at distance \(r\) from the axis, expressed in \(\text{kg} \cdot \text{m}^2\). While the polar moment of inertia measures an object's resistance to torsional deformation, the mass moment of inertia quantifies resistance to angular acceleration about an axis.
Applications in Mechanical Engineering
Polar moment of inertia quantifies an object's resistance to torsional deformation around a central axis, critical in designing shafts and rotating components subjected to twisting forces in mechanical engineering. Mass moment of inertia measures an object's resistance to angular acceleration about a specific axis, essential for analyzing rotational dynamics and stability in machinery such as flywheels, gears, and robotic arms. Engineers select the appropriate moment of inertia based on whether the application involves torsional stress analysis or rotational motion control to optimize performance and safety.
Role in Structural and Rotational Analysis
Polar moment of inertia quantifies an object's resistance to torsional deformation about an axis, essential for analyzing shear stress and twist in cylindrical shafts and structural members. Mass moment of inertia measures an object's resistance to angular acceleration around a rotational axis, key for dynamic analysis of rotating machinery and predicting rotational motion behavior. Both properties are critical in structural and rotational analysis but serve distinct purposes: polar moment relates to material distribution resisting torque, while mass moment relates to mass distribution governing angular motion.
Importance in Material Selection and Design
Polar moment of inertia and mass moment of inertia are critical in material selection and design for ensuring structural integrity and functional performance. Polar moment of inertia measures an object's resistance to torsion around an axis, influencing the choice of materials for shafts, beams, and circular components subjected to twisting forces. Mass moment of inertia quantifies resistance to angular acceleration, essential for optimizing rotating parts such as flywheels and gears by balancing weight distribution and material strength for efficient mechanical performance.
Real-world Examples and Case Studies
The polar moment of inertia is critical in analyzing torsional resistance in shafts used in automotive drive systems and aircraft propeller hubs, where torque and shear stress evaluation are vital for safety and performance. Mass moment of inertia plays a key role in dynamic behavior analysis of rotating machinery, such as flywheels in engines or rotor blades in wind turbines, influencing angular acceleration and stability. Case studies on helicopter rotor dynamics demonstrate how optimizing polar and mass moments of inertia enhances maneuverability and structural integrity under operational loads.
Summary and Comparative Insights
Polar moment of inertia measures an object's resistance to torsional deformation about an axis, quantifying the distribution of area relative to that axis, while mass moment of inertia quantifies an object's resistance to angular acceleration, based on the distribution of mass. The polar moment of inertia is critical in structural engineering for stress analysis under twisting loads, whereas mass moment of inertia is fundamental in dynamics and mechanical systems involving rotational motion. Comparing both, polar moment relates to geometric properties affecting shear stress, and mass moment depends on mass distribution influencing rotational kinetic energy.
Polar moment of inertia Infographic
 libterm.com
libterm.com