The damping ratio quantifies how oscillations in a system decay after a disturbance, playing a crucial role in controlling stability and vibration. Understanding this parameter helps optimize mechanical and structural designs to prevent excessive oscillations and ensure smooth performance. Explore the rest of the article to learn how your systems can achieve ideal damping for enhanced reliability.
Table of Comparison
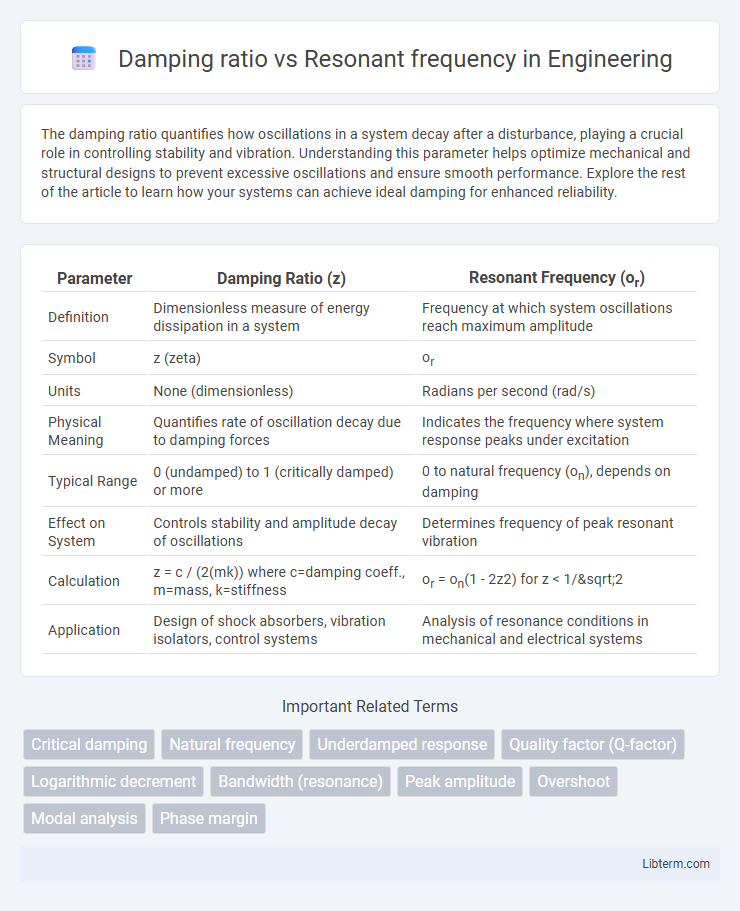
| Parameter | Damping Ratio (z) | Resonant Frequency (or) |
|---|---|---|
| Definition | Dimensionless measure of energy dissipation in a system | Frequency at which system oscillations reach maximum amplitude |
| Symbol | z (zeta) | or |
| Units | None (dimensionless) | Radians per second (rad/s) |
| Physical Meaning | Quantifies rate of oscillation decay due to damping forces | Indicates the frequency where system response peaks under excitation |
| Typical Range | 0 (undamped) to 1 (critically damped) or more | 0 to natural frequency (on), depends on damping |
| Effect on System | Controls stability and amplitude decay of oscillations | Determines frequency of peak resonant vibration |
| Calculation | z = c / (2(mk)) where c=damping coeff., m=mass, k=stiffness | or = on(1 - 2z2) for z < 1/&sqrt;2 |
| Application | Design of shock absorbers, vibration isolators, control systems | Analysis of resonance conditions in mechanical and electrical systems |
Introduction to Damping Ratio and Resonant Frequency
Damping ratio quantifies the degree of oscillation decay in a system, controlling how quickly vibrations diminish after a disturbance. Resonant frequency refers to the natural frequency at which a system oscillates with maximum amplitude when subjected to external periodic forces. Understanding the relationship between damping ratio and resonant frequency is crucial for optimizing system stability and performance in mechanical and electrical engineering applications.
Understanding Damping Ratio: Definition and Importance
Damping ratio quantifies the extent of energy dissipation in a vibrating system, crucial for controlling oscillation amplitude and system stability. It directly influences the resonant frequency, where higher damping ratios reduce the peak response at resonance, preventing excessive vibrations. Understanding this relationship is vital for designing mechanical systems, structures, and electronics to enhance performance and avoid resonance-induced failures.
Resonant Frequency Explained: Key Concepts
Resonant frequency is the natural frequency at which a system oscillates with maximum amplitude due to minimal energy loss, playing a critical role in mechanical, electrical, and structural systems. It is influenced by the system's mass and stiffness, with higher stiffness or lower mass resulting in a higher resonant frequency. Damping ratio affects how sharply a system resonates at this frequency, where low damping leads to pronounced resonance peaks, and high damping broadens the response curve, reducing vibration amplitudes near the resonant frequency.
Mathematical Relationship Between Damping Ratio and Resonant Frequency
The mathematical relationship between damping ratio (z) and resonant frequency (o_r) is defined by o_r = o_n (1 - z^2), where o_n is the natural frequency of the system. As the damping ratio increases, the resonant frequency decreases, indicating a shift of the peak response to lower frequencies. This relationship is crucial for analyzing the dynamic behavior of underdamped systems in mechanical and electrical engineering.
Impact of Damping Ratio on System Resonance
The damping ratio critically influences the system's resonant frequency by determining the amplitude and sharpness of resonance peaks. Higher damping ratios reduce resonant frequency amplitude and broaden the resonance curve, thereby minimizing vibration and oscillation risks in mechanical and structural systems. Accurate control of damping ratio is essential for optimizing system stability and preventing resonance-induced failures in engineering applications.
Effects of Resonant Frequency on System Dynamics
Resonant frequency critically influences system dynamics by determining the frequency at which the system oscillates with maximum amplitude, often resulting in heightened vibrations and potential structural fatigue. A higher resonant frequency typically correlates with stiffer, less damped systems, altering transient response and stability characteristics. Understanding this relationship enables precise tuning of mechanical and electrical systems to avoid resonance-induced failures and optimize performance.
Practical Applications: Damping Ratio vs Resonant Frequency
The damping ratio critically influences resonant frequency response, determining system stability and oscillation amplitude in mechanical and electrical systems. In practical applications such as automotive suspension design or vibration control in aerospace structures, optimizing the damping ratio minimizes resonance effects, enhancing performance and safety. Effective tuning of damping ratio relative to resonant frequency ensures energy dissipation and reduces the risk of structural failure or system malfunction under dynamic loads.
Comparing Underdamped, Critically Damped, and Overdamped Systems
In mechanical and electrical systems, the damping ratio (z) significantly influences the resonant frequency (or) and system response. Underdamped systems (0 < z < 1) exhibit oscillatory behavior with a resonant frequency slightly less than the natural frequency, while critically damped systems (z = 1) return to equilibrium as quickly as possible without oscillating, eliminating resonance peaks. Overdamped systems (z > 1) respond sluggishly with no oscillations and no defined resonant frequency, as energy dissipation dominates system dynamics.
Measurement Techniques for Damping Ratio and Resonant Frequency
Measurement techniques for damping ratio often involve logarithmic decrement, free vibration decay, or half-power bandwidth methods, where the system's response to excitation is analyzed to quantify energy dissipation. Resonant frequency is precisely determined using frequency sweep tests, impact hammer tests, or modal analysis, identifying peak amplitude points in the frequency response function. Both parameters require high-resolution sensors and signal processing tools such as FFT analyzers to extract accurate dynamic system characteristics essential for vibration analysis and structural health monitoring.
Optimizing System Performance: Finding the Right Balance
Damping ratio and resonant frequency are critical parameters in optimizing system performance, as the damping ratio controls energy dissipation while the resonant frequency determines the system's natural oscillation rate. Achieving the right balance between a low damping ratio and a high resonant frequency reduces oscillations and minimizes system vibrations, enhancing stability and response time. Precise adjustments to these factors improve overall efficiency in mechanical, electrical, and structural systems by preventing excessive resonance and ensuring smooth operation.
Damping ratio Infographic
 libterm.com
libterm.com