The Prandtl number is a dimensionless value that compares the rate of momentum diffusion to thermal diffusion in fluid flow, crucial for understanding heat transfer efficiency. It influences the boundary layer behavior in convection processes, impacting cooling and heating system designs. Explore the rest of the article to learn how the Prandtl number affects your engineering applications and fluid dynamics analysis.
Table of Comparison
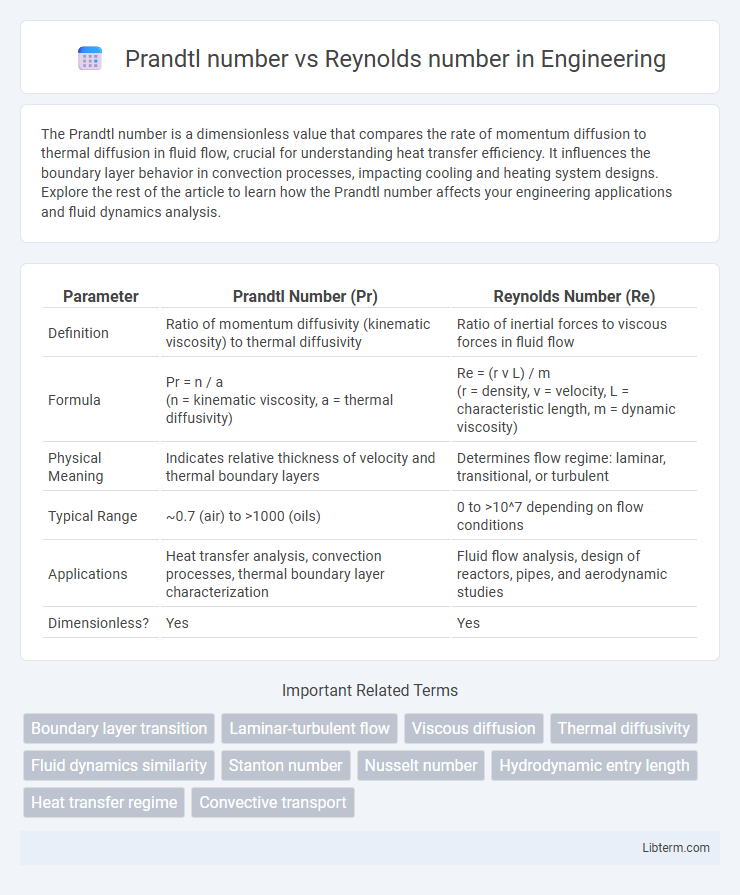
| Parameter | Prandtl Number (Pr) | Reynolds Number (Re) |
|---|---|---|
| Definition | Ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity | Ratio of inertial forces to viscous forces in fluid flow |
| Formula | Pr = n / a (n = kinematic viscosity, a = thermal diffusivity) |
Re = (r v L) / m (r = density, v = velocity, L = characteristic length, m = dynamic viscosity) |
| Physical Meaning | Indicates relative thickness of velocity and thermal boundary layers | Determines flow regime: laminar, transitional, or turbulent |
| Typical Range | ~0.7 (air) to >1000 (oils) | 0 to >10^7 depending on flow conditions |
| Applications | Heat transfer analysis, convection processes, thermal boundary layer characterization | Fluid flow analysis, design of reactors, pipes, and aerodynamic studies |
| Dimensionless? | Yes | Yes |
Understanding Prandtl Number: Definition and Significance
The Prandtl number (Pr) is a dimensionless quantity representing the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity, crucial for characterizing heat transfer in fluid flows. It influences the thickness of velocity and thermal boundary layers, directly impacting convection heat transfer calculations. Understanding the Prandtl number alongside the Reynolds number, which measures inertial versus viscous forces, enables engineers to predict flow regimes and optimize thermal system performance efficiently.
Reynolds Number Explained: Fundamentals and Importance
Reynolds number quantifies the ratio of inertial forces to viscous forces within a fluid flow, serving as a critical parameter to predict flow regimes such as laminar, transitional, or turbulent. It is calculated by the formula Re = ruL/m, where r represents fluid density, u is flow velocity, L is characteristic length, and m is dynamic viscosity, providing insight into flow behavior around objects and within channels. Understanding Reynolds number enables engineers to design efficient systems by optimizing fluid dynamics in applications ranging from aerospace to chemical processing.
Key Differences Between Prandtl and Reynolds Numbers
Prandtl number (Pr) represents the ratio of momentum diffusivity to thermal diffusivity and is primarily used to characterize heat transfer in fluid flows. Reynolds number (Re) measures the ratio of inertial forces to viscous forces, indicating the transition between laminar and turbulent flow regimes. Unlike Reynolds number, which governs flow behavior, Prandtl number specifically relates fluid properties affecting thermal and momentum boundary layer thicknesses.
Physical Interpretation of Prandtl Number in Fluid Flow
The Prandtl number (Pr) represents the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity in fluid flow, highlighting how velocity and temperature fields interact within a boundary layer. A high Pr value indicates that momentum diffuses more rapidly than heat, causing a thinner thermal boundary layer compared to the velocity boundary layer. In contrast, a low Prandtl number implies thermal energy diffuses quickly relative to momentum, affecting heat transfer characteristics in convective flows.
Reynolds Number: Laminar vs Turbulent Flow Criteria
The Reynolds number is a dimensionless quantity used to predict flow regimes in fluid dynamics, with laminar flow typically occurring at Re < 2300 and turbulent flow at Re > 4000. Flow behavior between these thresholds is considered transitional, where fluctuations increase before fully developed turbulence emerges. Understanding the Reynolds number is critical for engineering applications, as laminar flow is characterized by smooth, orderly fluid motion, whereas turbulent flow exhibits chaotic and vortical structures affecting heat and mass transfer rates.
Impact of Prandtl Number on Heat Transfer Processes
The Prandtl number (Pr) significantly influences heat transfer by characterizing the relative thickness of momentum and thermal boundary layers in fluid flow, where a higher Pr indicates a thicker velocity boundary layer compared to the thermal boundary layer. In turbulent flows with high Reynolds numbers (Re), the Prandtl number determines the rate of heat diffusion relative to momentum diffusion, affecting convective heat transfer coefficients. Understanding the interaction between Pr and Re enables optimization of thermal systems by predicting temperature distribution and improving the efficiency of heat exchangers and cooling processes.
Reynolds Number’s Role in Predicting Flow Regimes
Reynolds number is a dimensionless quantity crucial for characterizing fluid flow regimes by comparing inertial forces to viscous forces, thereby predicting whether flow will be laminar or turbulent. It is calculated as the ratio of fluid velocity, characteristic length, and fluid density to dynamic viscosity, with typical critical values around 2300 marking the transition between flow states. In contrast, the Prandtl number relates momentum diffusivity to thermal diffusivity, primarily influencing heat transfer characteristics rather than flow regime prediction.
Comparative Analysis: Prandtl Number vs Reynolds Number in Engineering Applications
Prandtl number (Pr), a dimensionless quantity representing the ratio of momentum diffusivity to thermal diffusivity, directly influences heat transfer characteristics in fluid flows, while Reynolds number (Re) quantifies the ratio of inertial forces to viscous forces, governing flow regimes. In engineering applications, Prandtl number is critical in designing heat exchangers and predicting thermal boundary layer behavior, whereas Reynolds number is essential for determining flow transitions, pressure drops, and turbulence modeling. Comparative analysis highlights that coupling Pr and Re enables optimized thermal-fluid system designs, ensuring accurate prediction of convective heat transfer and fluid flow dynamics.
Real-World Examples Demonstrating Prandtl and Reynolds Numbers
In fluid dynamics, the Prandtl number (Pr) characterizes the ratio of momentum diffusivity to thermal diffusivity, essential in heat transfer analysis, while the Reynolds number (Re) indicates the flow regime, distinguishing between laminar and turbulent flow. Real-world examples include air conditioning systems where low Prandtl numbers facilitate efficient thermal diffusion, and high Reynolds numbers in airplane wings cause turbulent airflow affecting lift and drag. Industrial processes like oil refining also demonstrate the interplay of Pr and Re numbers, optimizing heat exchangers and pipeline design for energy efficiency.
Summary Table: Prandtl Number vs Reynolds Number at a Glance
The Prandtl number (Pr) quantifies the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity, essential for analyzing heat transfer in fluid flows, while the Reynolds number (Re) measures the ratio of inertial forces to viscous forces, determining flow regimes such as laminar or turbulent flow. A summary table comparing Prandtl and Reynolds numbers highlights their distinct roles: Prandtl number is crucial for characterizing thermal boundary layers, typically ranging from 0.7 (air) to over 7,000 (engine oil), whereas Reynolds number spans from low values indicating laminar flow (Re < 2,300) to high values signifying turbulence (Re > 4,000). Together, these dimensionless numbers facilitate the prediction and modeling of heat transfer and fluid flow behavior across various engineering applications.
Prandtl number Infographic
 libterm.com
libterm.com