Unsteady state refers to a condition in which variables such as temperature, pressure, or concentration change with time within a system. This dynamic behavior is crucial in understanding processes in engineering, physics, and environmental studies where equilibrium is not achieved instantly. Explore the rest of the article to learn how unsteady state impacts your technical applications and problem-solving strategies.
Table of Comparison
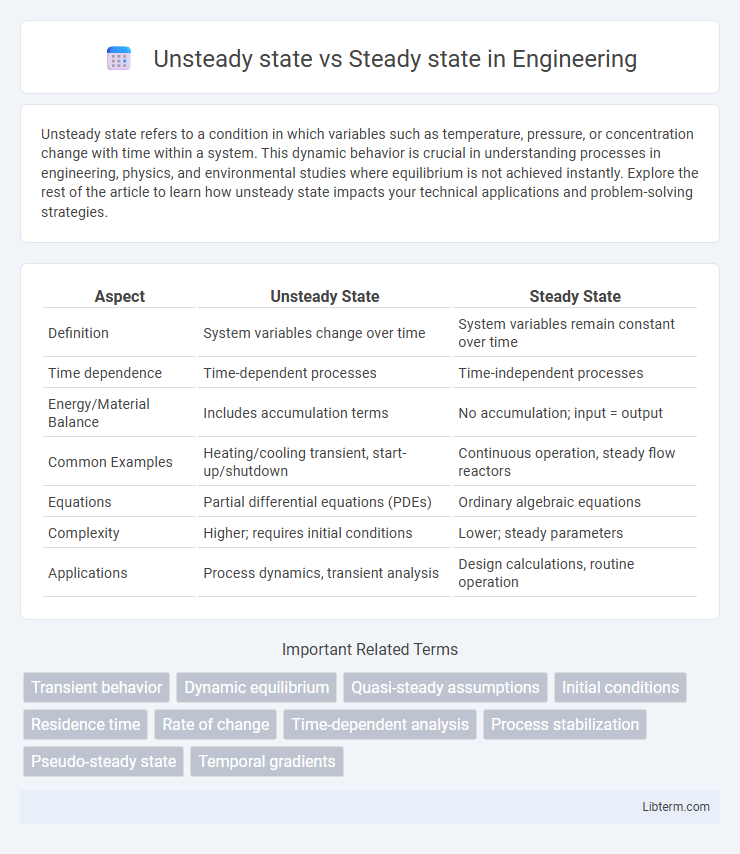
| Aspect | Unsteady State | Steady State |
|---|---|---|
| Definition | System variables change over time | System variables remain constant over time |
| Time dependence | Time-dependent processes | Time-independent processes |
| Energy/Material Balance | Includes accumulation terms | No accumulation; input = output |
| Common Examples | Heating/cooling transient, start-up/shutdown | Continuous operation, steady flow reactors |
| Equations | Partial differential equations (PDEs) | Ordinary algebraic equations |
| Complexity | Higher; requires initial conditions | Lower; steady parameters |
| Applications | Process dynamics, transient analysis | Design calculations, routine operation |
Introduction to Steady State and Unsteady State
Steady state refers to a condition where system variables such as temperature, pressure, or concentration remain constant over time despite ongoing processes. Unsteady state occurs when these variables change with time, reflecting transient or dynamic conditions within the system. Understanding the distinction between steady state and unsteady state is crucial for analyzing heat transfer, fluid flow, and chemical reaction systems effectively.
Defining Steady State: Key Characteristics
Steady state refers to a condition in a system where all variables remain constant over time despite ongoing processes, indicating equilibrium in flow rates, temperature, or concentration. Key characteristics include time-invariant properties, balanced input and output rates, and no accumulation or depletion of mass or energy within the system. This contrasts with unsteady state, where variables change dynamically due to transient conditions or system disturbances.
Understanding Unsteady State: Core Concepts
Unsteady state refers to conditions where system variables such as temperature, pressure, or concentration change with time, unlike steady state where these variables remain constant. In unsteady state analysis, transient behaviors and time-dependent differential equations are crucial for predicting system responses accurately. Understanding core concepts of unsteady state helps optimize dynamic processes in engineering, environmental studies, and chemical reactions.
Differences Between Steady State and Unsteady State
Steady state occurs when system variables such as temperature, pressure, and concentration remain constant over time, indicating equilibrium in the processes involved. Unsteady state, or transient state, involves changes in these variables as the system responds to external or internal disturbances before reaching equilibrium. The key difference lies in the time dependency of system properties: steady state shows no temporal variation, while unsteady state reflects continuous change until a new steady state is achieved.
Mathematical Modeling: Steady vs. Unsteady State
Mathematical modeling of steady state assumes system variables remain constant over time, leading to simplified algebraic equations representing equilibrium conditions. In contrast, unsteady state modeling incorporates time-dependent differential equations to capture dynamic changes in variables, reflecting transient behavior. Steady state models are often easier to solve but unsteady state models provide a more accurate representation of real systems undergoing temporal variations.
Real-World Examples of Steady State Systems
Steady state systems maintain constant conditions over time, exemplified by the Earth's climate regulation where energy input from the sun balances energy radiated back into space, resulting in a relatively stable global temperature. Industrial processes such as chemical reactors often operate in steady state, ensuring consistent product quality by maintaining fixed temperature, pressure, and concentration levels. Electrical circuits powered by a constant voltage source also achieve steady state when currents and voltages remain stable despite minor fluctuations in load.
Industrial Applications of Unsteady State Processes
Unsteady state processes are crucial in industries such as chemical reactors, heat exchangers, and environmental systems where conditions like temperature, pressure, and concentration change over time to optimize product yield and energy efficiency. In contrast, steady state assumes constant conditions, which is often unrealistic during startup, shutdown, or transient operation phases in manufacturing plants. Industrial applications leverage unsteady state modeling to improve process control, safety, and dynamic response in complex systems like batch reactors and catalytic converters.
Transitioning from Unsteady to Steady State
Transitioning from unsteady state to steady state involves the system stabilizing as transient effects dissipate and variables such as temperature, pressure, or concentration reach equilibrium. Monitoring the time-dependent changes during this phase is crucial for accurately predicting steady-state behavior in processes like chemical reactions or heat transfer. Advanced modeling techniques and real-time data analysis enhance understanding of the rate and conditions under which steady state is achieved.
Importance in Engineering and Process Design
Steady state conditions ensure consistent system behavior, enabling precise control and optimization in engineering processes, which is critical for reliable performance and energy efficiency. Unsteady state analysis is vital for understanding transient phenomena, system start-up, shutdown, and response to disturbances, informing safety measures and design resilience. Accurate modeling of both states supports robust process design, minimizing operational risks and maximizing efficiency in industrial applications.
Conclusion: Choosing the Right Approach
Selecting between unsteady state and steady state analysis depends on the system's dynamics and the precision required for performance evaluation. Steady state modeling is ideal for long-term operation scenarios where conditions remain constant, offering simplified calculations and faster results. Unsteady state analysis is essential for transient or dynamic systems to capture time-dependent behaviors accurately, ensuring robust design and control in fluctuating environments.
Unsteady state Infographic
 libterm.com
libterm.com