A damping matrix plays a crucial role in structural dynamics by representing energy dissipation through internal friction or external resistance. It influences system stability and response to vibrations, critical in engineering applications like earthquake analysis and mechanical design. Explore further to understand how your structure's performance can be optimized by selecting the appropriate damping matrix.
Table of Comparison
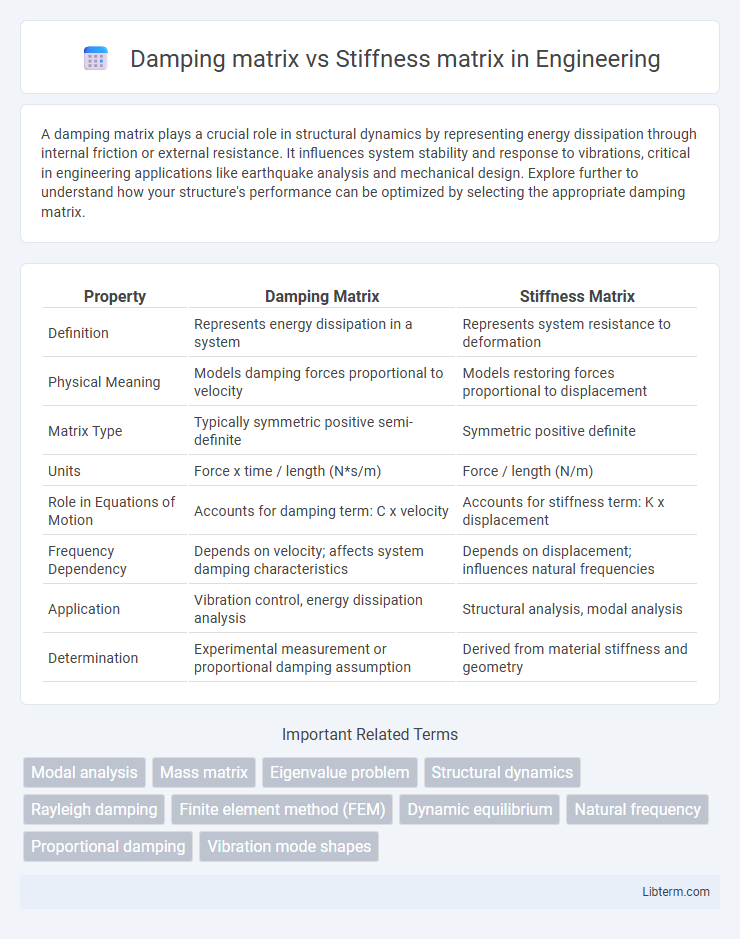
| Property | Damping Matrix | Stiffness Matrix |
|---|---|---|
| Definition | Represents energy dissipation in a system | Represents system resistance to deformation |
| Physical Meaning | Models damping forces proportional to velocity | Models restoring forces proportional to displacement |
| Matrix Type | Typically symmetric positive semi-definite | Symmetric positive definite |
| Units | Force x time / length (N*s/m) | Force / length (N/m) |
| Role in Equations of Motion | Accounts for damping term: C x velocity | Accounts for stiffness term: K x displacement |
| Frequency Dependency | Depends on velocity; affects system damping characteristics | Depends on displacement; influences natural frequencies |
| Application | Vibration control, energy dissipation analysis | Structural analysis, modal analysis |
| Determination | Experimental measurement or proportional damping assumption | Derived from material stiffness and geometry |
Introduction to Damping and Stiffness Matrices
The damping matrix represents energy dissipation in dynamic systems, quantifying how vibrations diminish over time and is critical in predicting system response under dynamic loading. The stiffness matrix defines the relationship between applied forces and resulting displacements, determining structural rigidity and deformation behavior. Both matrices are fundamental in finite element analysis for accurately modeling the mechanical behavior of structures under various dynamic and static conditions.
Fundamental Definitions
The damping matrix quantifies energy dissipation within a dynamic system, representing forces that oppose motion proportional to velocity, while the stiffness matrix characterizes the system's resistance to deformation, relating applied forces to displacements. These matrices are essential components in structural dynamics and finite element analysis, where the stiffness matrix defines elastic behavior and the damping matrix models viscous or structural damping effects. Understanding their fundamental definitions enables accurate simulation of mechanical response under dynamic loading conditions.
Physical Significance in Structural Dynamics
The damping matrix represents energy dissipation mechanisms that reduce vibrational amplitude over time, modeling material internal friction, air resistance, and other energy loss factors in structural dynamics. The stiffness matrix characterizes the resistance of structural elements to deformation under applied loads, defining the elastic restoring forces proportional to displacement. Together, these matrices describe the dynamic response of structures by balancing energy storage and energy dissipation during oscillations.
Mathematical Formulation
The damping matrix C in dynamic systems is commonly formulated as a linear combination of the mass matrix M and the stiffness matrix K, expressed as C = aM + bK, where a and b are damping coefficients that characterize energy dissipation. The stiffness matrix K represents the system's resistance to deformation and is derived from partial derivatives of the strain energy with respect to displacement, typically symmetric and positive definite in elastic systems. In contrast, the damping matrix C models energy loss mechanisms, often non-proportional, impacting modal analysis and system stability due to its potential non-symmetric nature in realistic damping scenarios.
Matrix Properties and Structure
The damping matrix typically exhibits symmetric and positive semi-definite properties, closely related to energy dissipation in dynamic systems, while the stiffness matrix is symmetric and positive definite, representing the system's resistance to deformation. Both matrices are square and of the same dimension as the degrees of freedom, but the stiffness matrix's structure is usually sparser due to localized connections in mechanical models. Eigenvalue analysis of the stiffness matrix yields natural frequencies, whereas the damping matrix influences modal damping ratios, highlighting their distinct roles in dynamic response.
Roles in Vibration Analysis
The damping matrix quantifies the energy dissipation mechanisms in a vibrating system, controlling how oscillations decay over time and influencing the system's transient response. The stiffness matrix represents the system's resistance to deformation, governing the natural frequencies and mode shapes critical for predicting vibration behavior. Together, these matrices define the dynamic characteristics of structures, enabling accurate vibration analysis and system stability assessment.
Comparison of Energy Dissipation and Storage
The damping matrix represents energy dissipation in mechanical systems by accounting for forces proportional to velocity, converting mechanical energy into heat or other forms, thereby reducing system vibrations. The stiffness matrix illustrates energy storage by quantifying the elastic forces proportional to displacement, enabling the system to store potential energy during deformation and recover it upon release. Comparing the two, the damping matrix governs energy loss and attenuation, while the stiffness matrix controls energy retention and system stability.
Influence on System Behavior
The damping matrix influences system behavior by controlling energy dissipation and affecting the rate at which oscillations decay, thereby stabilizing dynamic responses. The stiffness matrix defines the system's resistance to deformation, governing natural frequencies and mode shapes critical for vibration analysis. Together, these matrices determine the stability, transient response, and resonance characteristics of mechanical and structural systems.
Applications in Engineering
The damping matrix models energy dissipation in dynamic systems, essential for predicting vibration attenuation in structural engineering and automotive suspension design. The stiffness matrix represents the relationship between applied forces and resulting displacements, critical for finite element analysis in civil infrastructure and aerospace component design. Accurate integration of both matrices ensures stability and performance in modal analysis and control system simulations.
Summary: Key Differences and Similarities
The damping matrix represents energy dissipation mechanisms in dynamic systems, while the stiffness matrix characterizes resistance to deformation under static loads. Both matrices are square and symmetric in linear structural analysis, contributing to the system's equations of motion. The damping matrix primarily affects system response over time by influencing vibration decay, whereas the stiffness matrix determines displacement magnitudes under applied forces.
Damping matrix Infographic
 libterm.com
libterm.com