Forced oscillation occurs when an external periodic force drives a system to oscillate at a specific frequency, overriding its natural frequency. This concept is crucial in understanding phenomena such as resonance, where the amplitude of oscillations significantly increases, potentially causing structural damage or failure. Discover how forced oscillation impacts various mechanical and electrical systems by reading the rest of the article.
Table of Comparison
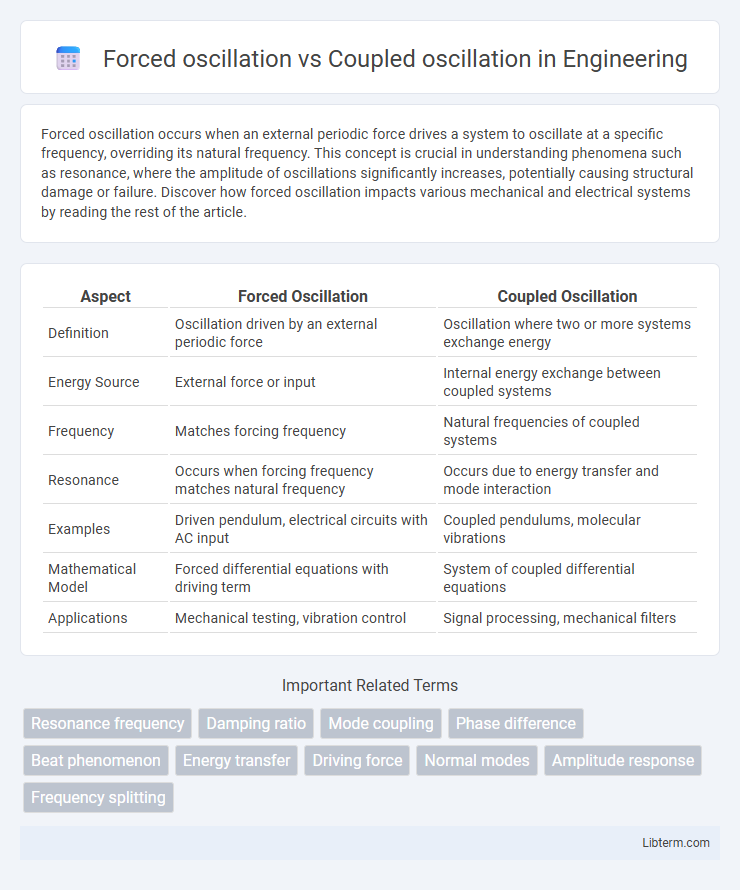
| Aspect | Forced Oscillation | Coupled Oscillation |
|---|---|---|
| Definition | Oscillation driven by an external periodic force | Oscillation where two or more systems exchange energy |
| Energy Source | External force or input | Internal energy exchange between coupled systems |
| Frequency | Matches forcing frequency | Natural frequencies of coupled systems |
| Resonance | Occurs when forcing frequency matches natural frequency | Occurs due to energy transfer and mode interaction |
| Examples | Driven pendulum, electrical circuits with AC input | Coupled pendulums, molecular vibrations |
| Mathematical Model | Forced differential equations with driving term | System of coupled differential equations |
| Applications | Mechanical testing, vibration control | Signal processing, mechanical filters |
Introduction to Oscillation Phenomena
Forced oscillation occurs when an external periodic force drives a system, causing it to oscillate at the frequency of the applied force, often resulting in resonance when this frequency matches the system's natural frequency. Coupled oscillation involves two or more oscillators linked in such a way that energy transfers between them, producing complex motion patterns including normal modes where oscillators move synchronously. Understanding these oscillation phenomena is fundamental in fields like mechanical engineering, physics, and signal processing for analyzing dynamic system behaviors.
Defining Forced Oscillation
Forced oscillation occurs when an external periodic force drives a system to oscillate at the frequency of the applied force, overriding the system's natural frequency. This phenomenon contrasts with coupled oscillation, where two or more oscillators interact and exchange energy, leading to synchronized oscillations without external forcing. Forced oscillation is critical in understanding resonance, as the amplitude of oscillation significantly increases when the driving frequency matches the system's natural frequency.
Understanding Coupled Oscillation
Coupled oscillation occurs when two or more oscillators interact and exchange energy, resulting in synchronized or complex motion patterns. Unlike forced oscillation, where an external periodic force drives a single oscillator, coupled oscillators influence each other's frequencies and amplitudes through their connection. This interaction leads to phenomena such as mode splitting, energy transfer, and the emergence of normal modes characterized by collective oscillations at specific frequencies.
Key Mechanisms: Forcing vs. Coupling
Forced oscillation involves an external periodic force driving the system, causing oscillations at the frequency of the applied force, with energy input directly sustaining motion. Coupled oscillation arises from interaction between two or more oscillators linked by a restoring force, allowing energy exchange and creating normal modes with characteristic frequencies. The key mechanism difference is that forced oscillation depends on external input for motion, while coupled oscillation results from intrinsic dynamic interactions between oscillators.
Mathematical Representation
Forced oscillation is mathematically described by a second-order differential equation with an external driving force term, typically written as m d2x/dt2 + b dx/dt + kx = F0 cos(ot), where m is mass, b is damping coefficient, k is spring constant, and F0 cos(ot) represents the periodic external force. Coupled oscillations involve systems of two or more interacting oscillators represented by simultaneous differential equations, such as m1 d2x1/dt2 + k1 x1 + k_c (x1 - x2) = 0 and m2 d2x2/dt2 + k2 x2 + k_c (x2 - x1) = 0, where k_c denotes coupling stiffness. The eigenvalues of the coefficient matrix in coupled oscillations determine the normal modes and frequencies, contrasting with forced oscillations where the solution consists of homogeneous and particular parts reflecting natural and driven frequencies.
Energy Transfer in Each System
Forced oscillations involve an external periodic force driving the system, leading to continuous energy input and transfer from the driving source to the oscillating object, often resulting in resonance when frequencies match. Coupled oscillations feature two or more interacting oscillators exchanging energy back and forth internally through their coupling, without external energy input once motion begins. Energy transfer in coupled oscillators occurs via the coupling mechanism, causing oscillation amplitudes to vary and energy to oscillate between components over time.
Resonance Comparison
Forced oscillation occurs when an external periodic force drives a system, leading to resonance at the driving frequency when it matches the system's natural frequency, causing a significant amplitude increase. Coupled oscillation involves two or more interacting oscillators exchanging energy, with resonance manifesting as coupled modes where energy transfer peaks at characteristic frequencies. Resonance in forced oscillation results in a single dominant frequency amplification, while in coupled oscillation, resonance leads to complex mode splitting and multiple resonant frequencies based on the coupling strength.
Real-World Examples
Forced oscillation occurs when an external periodic force drives a system, such as a child on a swing pushed at regular intervals or the vibrations of a bridge caused by rhythmic foot traffic. Coupled oscillation involves two or more interconnected oscillators influencing each other's motion, exemplified by the synchronized flashing of fireflies or the coupled pendulums in a grandfather clock. These phenomena illustrate fundamental principles in mechanical engineering, electronics, and even biological systems, where energy transfer and resonance play critical roles.
Practical Applications and Implications
Forced oscillation systems are widely utilized in engineering applications such as vibration control in automotive suspensions and seismic dampers in buildings, where external periodic forces drive system responses to specific frequencies. Coupled oscillation phenomena are critical in designing synchronized networks, including power grids and laser arrays, enabling coherent energy transfer and stable operation. Understanding the differences aids in optimizing system stability, energy efficiency, and response precision across mechanical, electrical, and structural engineering domains.
Summary: Differences and Similarities
Forced oscillation occurs when an external periodic force drives a system, maintaining its motion even with energy loss, whereas coupled oscillation involves energy transfer between two or more interconnected oscillators influencing each other's motion. Both phenomena exhibit periodic motion and can experience resonance, but forced oscillations rely on external driving forces while coupled oscillations arise from the interaction within the system components. Understanding their differences and similarities is crucial in mechanical and electrical system design to control vibration and wave propagation.
Forced oscillation Infographic
 libterm.com
libterm.com