Monte Carlo simulation uses random sampling to model complex systems and assess the impact of risk and uncertainty in predictive forecasting. This method is widely applied in finance, engineering, and project management to evaluate potential outcomes and inform decision-making processes. Explore the rest of the article to understand how Monte Carlo simulation can enhance your analysis and improve accuracy.
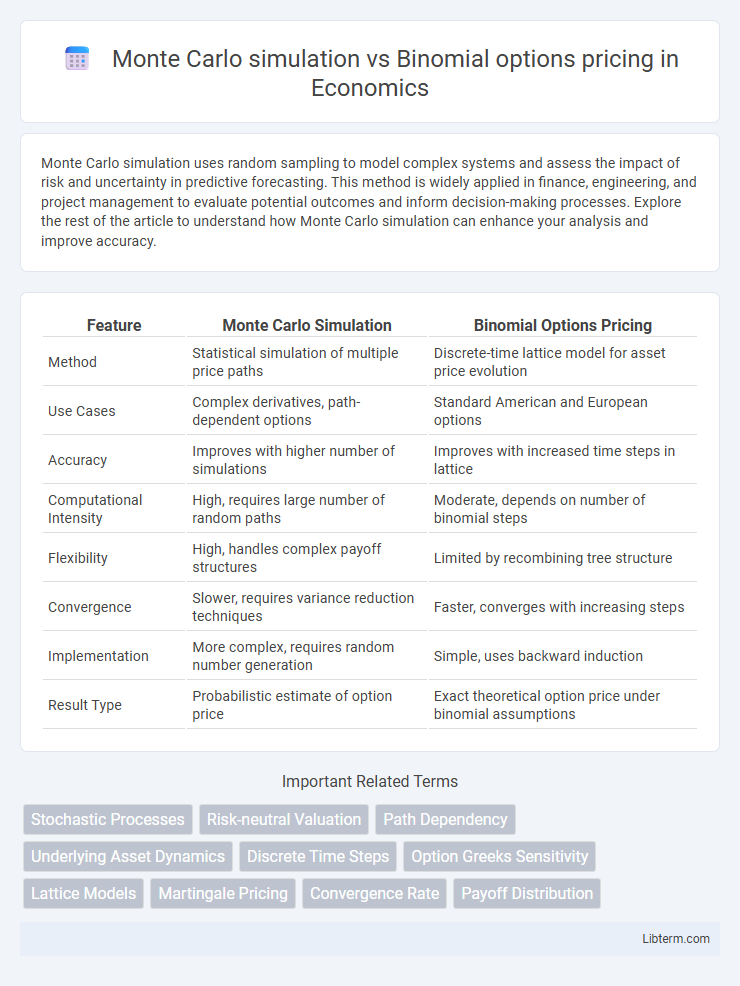
Table of Comparison
| Feature | Monte Carlo Simulation | Binomial Options Pricing |
|---|---|---|
| Method | Statistical simulation of multiple price paths | Discrete-time lattice model for asset price evolution |
| Use Cases | Complex derivatives, path-dependent options | Standard American and European options |
| Accuracy | Improves with higher number of simulations | Improves with increased time steps in lattice |
| Computational Intensity | High, requires large number of random paths | Moderate, depends on number of binomial steps |
| Flexibility | High, handles complex payoff structures | Limited by recombining tree structure |
| Convergence | Slower, requires variance reduction techniques | Faster, converges with increasing steps |
| Implementation | More complex, requires random number generation | Simple, uses backward induction |
| Result Type | Probabilistic estimate of option price | Exact theoretical option price under binomial assumptions |
Introduction to Options Pricing Models
Monte Carlo simulation and Binomial options pricing are essential models used to estimate the fair value of options by accounting for underlying asset price dynamics and market uncertainties. The Binomial model constructs a discrete-time lattice of possible asset price movements, providing a flexible framework for American and European options with varying exercise features. Monte Carlo simulation relies on generating numerous random price paths through stochastic processes, offering high accuracy in pricing complex derivatives and path-dependent options where analytical solutions are difficult.
Overview of Monte Carlo Simulation
Monte Carlo simulation is a statistical technique used to model the probability of different outcomes in complex financial instruments by running thousands or millions of random price path simulations. It is highly effective for valuing options with multiple sources of uncertainty or path-dependent features, unlike the binomial options pricing model which relies on discrete time-steps and simpler assumptions. This simulation harnesses stochastic processes to capture the full distribution of possible asset returns, providing a flexible and robust framework for option valuation.
Fundamentals of the Binomial Options Pricing Model
The Binomial Options Pricing Model relies on a discrete-time framework where the price of the underlying asset can move up or down by specific factors at each step until the option's expiration. This methodology uses a recombining price tree to evaluate all possible paths, enabling the calculation of option values through risk-neutral probabilities and backward induction. Monte Carlo simulation, in contrast, uses random sampling to model price paths, making it computationally intensive but flexible for complex derivatives, whereas the binomial model is particularly effective for American options and early exercise features due to its lattice structure.
Key Assumptions of Each Method
Monte Carlo simulation assumes a continuous stochastic process, typically geometric Brownian motion, to model underlying asset price paths, capturing complex option features and path dependencies. Binomial options pricing relies on a discrete-time, recombining lattice framework, assuming a fixed up or down movement per time step with risk-neutral probabilities, enabling efficient valuation of American-style options. Each method's precision depends on assumptions about volatility, time intervals, and market behavior, influencing computational complexity and suitability for different option types.
Mathematical Frameworks Compared
The Monte Carlo simulation uses stochastic processes to model numerous potential future price paths of the underlying asset, applying random sampling to estimate the expected payoff of an option. In contrast, the Binomial options pricing model constructs a discrete-time lattice to represent potential asset price movements, calculating option value through backward induction by evaluating payoff at each node. While Monte Carlo excels in handling complex derivatives and path-dependent options, the binomial model offers computational simplicity and closed-form approximations for American-style options.
Computational Complexity and Efficiency
Monte Carlo simulation involves generating a large number of random sample paths to estimate option prices, resulting in high computational complexity that scales with the number of simulations and time steps, often making it less efficient for real-time pricing. In contrast, the Binomial options pricing model uses a discrete-time lattice framework with a fixed number of steps, providing a more computationally efficient approach for American and European options while maintaining accuracy. The binomial model's complexity grows linearly with the number of nodes, making it faster and more efficient for relatively simpler payoff structures compared to the Monte Carlo method's reliance on stochastic sampling.
Accuracy and Use Cases
Monte Carlo simulation provides higher accuracy for complex derivative pricing by modeling a wide range of possible price paths and incorporating multiple sources of uncertainty, making it ideal for exotic options and portfolio risk analysis. The Binomial options pricing model offers a simpler, computationally efficient approach with reliable results for American and European options under less complex conditions, especially when the number of time steps is sufficiently large. Monte Carlo is preferred in scenarios requiring detailed risk assessment and path-dependent features, while the Binomial model suits fast calculations and early exercise decisions in standard options.
Applications in Exotic and American Options
Monte Carlo simulation excels in pricing exotic and American options by handling complex path-dependent features and early exercise opportunities that binomial option pricing models struggle with due to their discrete time steps and lattice structure. The flexibility of Monte Carlo methods allows for accurate valuation of options with multiple sources of uncertainty and stochastic processes, making it particularly valuable for exotic derivatives such as Asian, Barrier, and Lookback options. While binomial models provide intuitive and computationally efficient solutions for American options in simpler cases, Monte Carlo techniques combined with regression methods (e.g., Longstaff-Schwartz algorithm) offer superior performance in high-dimensional problems and sophisticated payoff structures.
Strengths and Weaknesses of Each Approach
Monte Carlo simulation excels in handling complex, path-dependent options and capturing a wide range of market conditions by simulating numerous possible price paths, providing flexibility at the cost of high computational intensity and longer processing times. Binomial options pricing offers a simpler, discrete-time model that is easier to implement and interpret, ideal for American options with early exercise features, but it may become less accurate or computationally expensive as the number of time steps increases. Monte Carlo is preferred for high-dimensional problems, while the binomial method is more efficient for lower-dimensional, simpler payoff structures.
Choosing the Right Model: Practical Considerations
Monte Carlo simulation offers flexibility in modeling complex, path-dependent options with multiple sources of uncertainty, making it suitable for American and exotic options where early exercise and varying payoffs occur. Binomial options pricing provides a discrete, lattice-based method that is computationally efficient and ideal for simpler European and American options with well-defined payoffs and exercise boundaries. Practical considerations in choosing the right model hinge on option complexity, computational resources, convergence speed, and the need for accurate Greeks estimation.
Monte Carlo simulation Infographic
 libterm.com
libterm.com