The VES (Variable Elasticity of Substitution) production function captures how the ease of substituting between inputs can change depending on their relative quantities, offering a more flexible representation than constant elasticity models. This feature allows it to model production processes where input substitutability is not fixed, reflecting more realistic economic scenarios. Discover how this approach can enhance your understanding of production dynamics by reading the rest of the article.
Table of Comparison
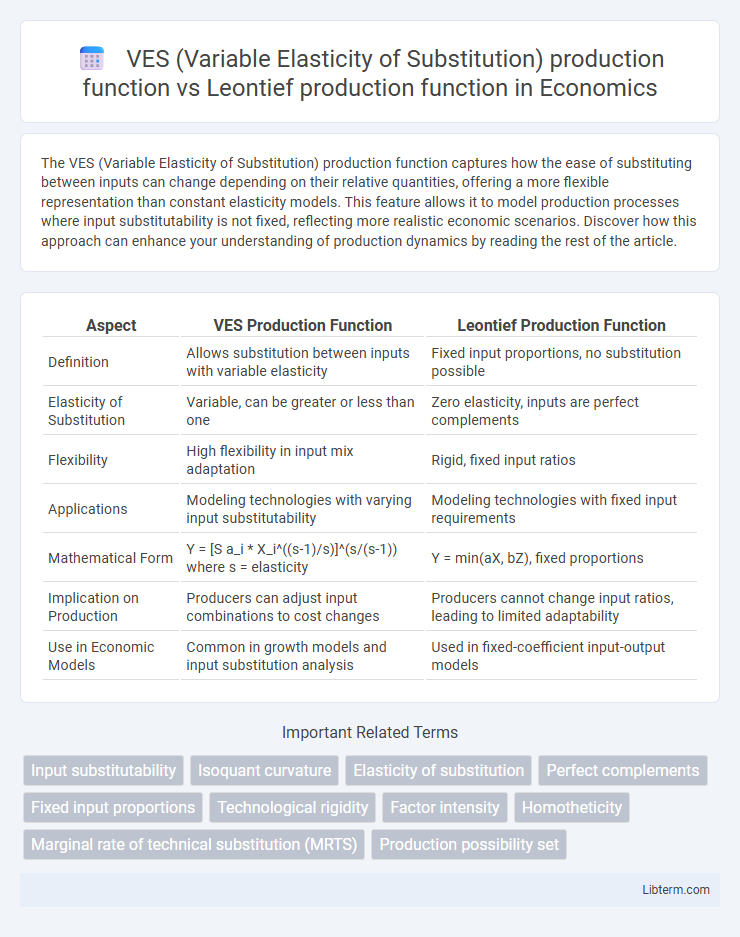
| Aspect | VES Production Function | Leontief Production Function |
|---|---|---|
| Definition | Allows substitution between inputs with variable elasticity | Fixed input proportions, no substitution possible |
| Elasticity of Substitution | Variable, can be greater or less than one | Zero elasticity, inputs are perfect complements |
| Flexibility | High flexibility in input mix adaptation | Rigid, fixed input ratios |
| Applications | Modeling technologies with varying input substitutability | Modeling technologies with fixed input requirements |
| Mathematical Form | Y = [S a_i * X_i^((s-1)/s)]^(s/(s-1)) where s = elasticity | Y = min(aX, bZ), fixed proportions |
| Implication on Production | Producers can adjust input combinations to cost changes | Producers cannot change input ratios, leading to limited adaptability |
| Use in Economic Models | Common in growth models and input substitution analysis | Used in fixed-coefficient input-output models |
Introduction to Production Functions
The Variable Elasticity of Substitution (VES) production function generalizes input substitutability by allowing the elasticity of substitution to vary between inputs, offering greater flexibility in modeling different production technologies. In contrast, the Leontief production function assumes perfect complementarity with a fixed input ratio, representing zero elasticity of substitution and strict input proportions. These differences highlight the VES function's ability to capture nuanced substitution effects compared to the rigid structure of the Leontief function in production analysis.
Overview of VES (Variable Elasticity of Substitution) Production Function
The VES (Variable Elasticity of Substitution) production function allows for a flexible substitution between inputs, adapting the elasticity of substitution based on input ratios, which contrasts with the fixed substitution characteristic of the Leontief production function. VES captures varying degrees of complementarity and substitutability among inputs, making it suitable for modeling diverse production technologies where input flexibility is crucial. This adaptability enhances its application in economic analyses involving shifts in input usage patterns and cost structures, unlike the rigid input proportions assumed in the Leontief framework.
Key Features of the Leontief Production Function
The Leontief production function is characterized by fixed input coefficients, representing a rigid, no-substitution technology where inputs are used in strict proportions. Unlike the VES (Variable Elasticity of Substitution) production function, which allows elasticity of substitution to vary and can adapt to different input substitution rates, the Leontief function assumes zero substitutability between inputs. This rigidity makes the Leontief production function particularly useful for modeling industries or processes with inflexible input combinations and limited technological flexibility.
Mathematical Formulation: VES vs Leontief
The VES (Variable Elasticity of Substitution) production function is mathematically expressed as \( Q = \left(\sum_{i} a_i X_i^{\rho}\right)^{\frac{1}{\rho}} \), where \( \rho \) controls the elasticity of substitution between inputs, allowing flexibility in input substitutability. The Leontief production function, defined as \( Q = \min\left(\frac{X_1}{a_1}, \frac{X_2}{a_2}, \dots, \frac{X_n}{a_n}\right) \), assumes zero substitutability, reflecting fixed-proportion input requirements. The VES function generalizes input relationships by adjusting \( \rho \), whereas the Leontief function models perfect complementarity with no input substitution.
Substitution Elasticity: Variable vs Fixed
The VES (Variable Elasticity of Substitution) production function allows substitution elasticity to change with input proportions, providing flexibility in modeling varied input combinations and their efficiency. The Leontief production function assumes a fixed substitution elasticity of zero, implying perfect complementarity between inputs with no ability to substitute one input for another. This fundamental difference makes the VES function more adaptable in capturing real-world production scenarios where input interchangeability varies.
Flexibility in Input Utilization
The VES (Variable Elasticity of Substitution) production function offers greater flexibility in input utilization by allowing the elasticity of substitution between inputs to change, adapting to varying production conditions. In contrast, the Leontief production function assumes fixed input proportions with zero substitutability, enforcing rigid input usage regardless of relative input prices. This fundamental difference makes VES more suitable for modeling technologies where input substitutability varies, while Leontief suits processes requiring strict input combinations.
Graphical Representation and Isoquants
VES production functions exhibit smoothly curved isoquants reflecting a variable rate of substitution between inputs, allowing flexibly shaped curves that adjust elasticity depending on input ratios. Leontief production functions have right-angled, L-shaped isoquants representing perfect complementarity with fixed input proportions and zero substitutability. Graphically, VES isoquants show continuous smooth convexity while Leontief isoquants form rigid corners indicating input requirements cannot be substituted for one another.
Real-World Applications and Examples
The VES (Variable Elasticity of Substitution) production function allows for flexible substitution between inputs, making it widely used in sectors like manufacturing and energy where input flexibility impacts efficiency under changing economic conditions. The Leontief production function, characterized by fixed input proportions, is commonly applied in industries such as construction and agriculture where input substitutability is minimal and production processes require strict input ratios. Real-world examples include VES modeling of capital-labor substitution in the automotive industry and Leontief analysis of input-output relationships in national economic planning.
Advantages and Limitations of Each Function
The VES (Variable Elasticity of Substitution) production function offers flexibility by allowing the elasticity of substitution between inputs to vary, enabling better modeling of production processes with changing input substitutability. Its advantage lies in capturing diverse technological conditions, but it may involve complex estimation and parameter identification challenges. The Leontief production function assumes fixed input proportions with zero substitutability, simplifying analysis and offering clear interpretation but limiting its applicability to industries where inputs cannot be substituted, thus reducing flexibility in representing real-world production scenarios.
Summary: Choosing the Right Production Function
The Variable Elasticity of Substitution (VES) production function offers flexibility by allowing the elasticity of substitution between inputs to vary, accommodating diverse technological scenarios and providing a more realistic representation of production processes. In contrast, the Leontief production function assumes fixed input proportions with zero substitutability, making it suitable for processes with rigid input requirements and no input flexibility. Selecting the appropriate production function depends on the nature of input substitutability and technological characteristics within the production system, influencing model accuracy and economic analysis outcomes.
VES (Variable Elasticity of Substitution) production function Infographic
 libterm.com
libterm.com