The Weber number is a dimensionless quantity used in fluid mechanics to characterize the relative importance of inertial forces compared to surface tension forces in fluid flow. It plays a crucial role in analyzing phenomena such as droplet formation, breakup, and bubble dynamics. Discover how understanding the Weber number can enhance your insights into fluid behavior throughout the rest of this article.
Table of Comparison
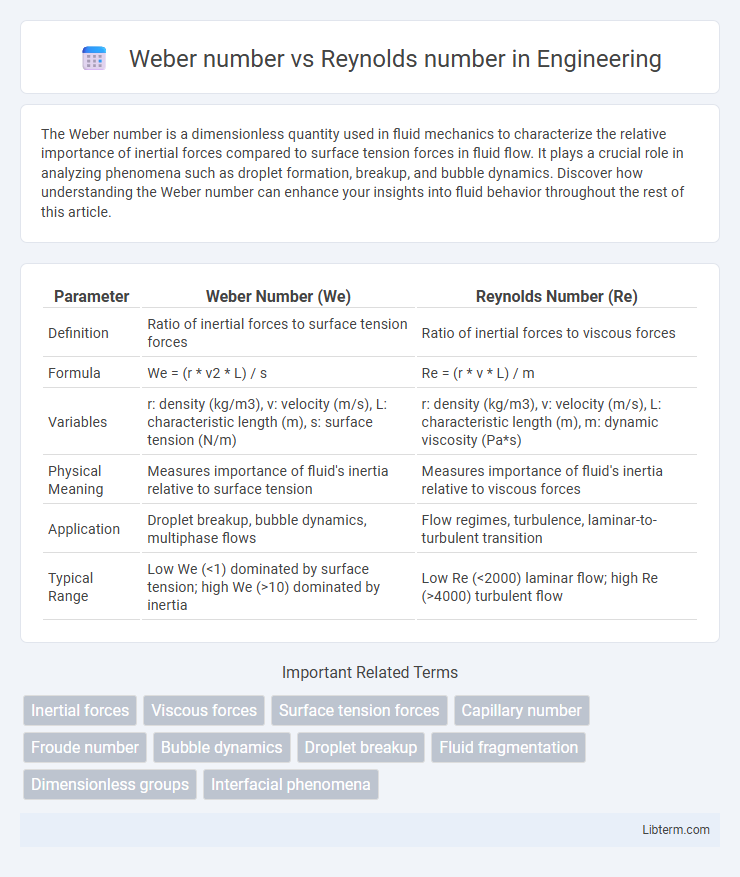
| Parameter | Weber Number (We) | Reynolds Number (Re) |
|---|---|---|
| Definition | Ratio of inertial forces to surface tension forces | Ratio of inertial forces to viscous forces |
| Formula | We = (r * v2 * L) / s | Re = (r * v * L) / m |
| Variables | r: density (kg/m3), v: velocity (m/s), L: characteristic length (m), s: surface tension (N/m) | r: density (kg/m3), v: velocity (m/s), L: characteristic length (m), m: dynamic viscosity (Pa*s) |
| Physical Meaning | Measures importance of fluid's inertia relative to surface tension | Measures importance of fluid's inertia relative to viscous forces |
| Application | Droplet breakup, bubble dynamics, multiphase flows | Flow regimes, turbulence, laminar-to-turbulent transition |
| Typical Range | Low We (<1) dominated by surface tension; high We (>10) dominated by inertia | Low Re (<2000) laminar flow; high Re (>4000) turbulent flow |
Introduction to Weber and Reynolds Numbers
Weber number and Reynolds number are dimensionless quantities fundamental to fluid mechanics, characterizing different aspects of fluid flow behavior. The Weber number measures the relative importance of inertial forces to surface tension forces in multiphase flows, essential in droplet and bubble dynamics. Reynolds number quantifies the ratio of inertial forces to viscous forces, indicating whether flow is laminar or turbulent in single-phase fluids.
Defining the Weber Number
The Weber number (We) quantifies the ratio of inertial forces to surface tension forces in fluid dynamics, particularly relevant in multiphase flows and droplet formation. It is mathematically expressed as We = ru2L/s, where r represents fluid density, u is characteristic velocity, L denotes characteristic length, and s is surface tension. In contrast, the Reynolds number (Re) compares inertial forces to viscous forces, emphasizing flow regime characterization rather than interfacial effects.
Understanding the Reynolds Number
Reynolds number quantifies the ratio of inertial forces to viscous forces in fluid flow, serving as a critical parameter to predict flow regimes such as laminar or turbulent flow. Unlike the Weber number, which relates inertial forces to surface tension and is vital in multiphase flows and droplet dynamics, the Reynolds number primarily influences momentum transfer and flow stability. Understanding the Reynolds number enables engineers to design efficient fluid systems by assessing resistance, mixing, and heat transfer characteristics in various applications.
Physical Significance: Weber vs Reynolds
Weber number quantifies the relative importance of fluid inertia compared to surface tension forces, essential in predicting droplet formation and breakup in multiphase flows. Reynolds number measures the ratio of inertial forces to viscous forces, determining flow regimes such as laminar or turbulent flow. Understanding the Weber number helps optimize spray and droplet dynamics, while the Reynolds number guides flow characterization and heat transfer efficiency in fluid systems.
Key Differences Between Weber and Reynolds Numbers
Weber number quantifies the ratio of inertial forces to surface tension forces in fluid dynamics, essential for analyzing droplet formation and breakup. Reynolds number measures the ratio of inertial forces to viscous forces, determining flow regimes such as laminar or turbulent flow. Key differences include Weber number's emphasis on surface tension effects versus Reynolds number's focus on viscous effects in fluid flow characterization.
Similarities and Overlapping Applications
The Weber number and Reynolds number both quantify fluid dynamics phenomena, with the Weber number emphasizing surface tension effects and the Reynolds number capturing inertial versus viscous forces. Both dimensionless numbers are crucial in analyzing multiphase flow, droplet dynamics, and bubble formation, often overlapping in applications such as spray atomization, emulsification, and capillary flow. Their joint use enables comprehensive prediction of flow regimes, stability, and breakup behavior in engineering and natural systems.
Practical Examples in Fluid Mechanics
The Weber number quantifies the relative importance of fluid inertia compared to surface tension, crucial in analyzing droplet formation, spray atomization, and bubble dynamics, while the Reynolds number measures the ratio of inertial to viscous forces, influencing flow regimes like laminar or turbulent flow in pipes and around airfoils. In practical fluid mechanics, the Weber number helps predict droplet breakup in fuel injectors and inkjet printers, whereas the Reynolds number guides the design of hydraulic systems and vehicles by characterizing flow resistance and stability. Understanding both numbers allows engineers to optimize processes involving multiphase flow and fluid-structure interactions in fields such as aerospace, chemical processing, and environmental engineering.
Importance in Engineering and Industry
The Weber number quantifies the relative importance of inertial forces to surface tension forces in fluid flow, critical for analyzing droplet formation, atomization, and multiphase flow processes in industries such as chemical engineering and fuel injection systems. The Reynolds number measures the ratio of inertial forces to viscous forces, guiding the prediction of flow regimes, turbulence, and heat transfer efficiency essential for pipeline design, aerodynamic performance, and HVAC systems. Both dimensionless numbers are fundamental for optimizing fluid dynamics applications, improving equipment performance, and ensuring safety in engineering solutions.
Calculation Methods and Formulas
The Weber number (We) is calculated using the formula We = r u2 L / s, where r represents fluid density, u is flow velocity, L denotes characteristic length, and s is surface tension. The Reynolds number (Re) is determined by Re = r u L / m, with m symbolizing fluid viscosity. Both dimensionless numbers quantify different fluid dynamics aspects: We compares inertial to surface tension forces, while Re measures inertial to viscous forces.
Summary and Key Takeaways
Weber number (We) quantifies the relative importance of fluid inertia compared to surface tension, critical in analyzing droplet formation and breakup in multiphase flows. Reynolds number (Re) measures the ratio of inertial forces to viscous forces, governing flow regimes like laminar or turbulent flow. Understanding the distinct roles of We and Re enables precise control over fluid dynamics in applications such as spray atomization, bubble dynamics, and emulsification processes.
Weber number Infographic
 libterm.com
libterm.com